C++实现矩阵原地转置算法
本文实例描述了C++实现矩阵原地转置算法,是一个非常经典的算法,相信对于学习C++算法的朋友有很大的帮助。具体如下:
一、问题描述
微软面试题:将一个MxN的矩阵存储在一个一维数组中,编程实现矩阵的转置。
要求:空间复杂度为O(1)
二、思路分析
下面以一个4x2的矩阵A={1,2,3,4,5,6,7,8}进行分析,转置过程如下图:

图中右下角的红色数字表示在一维数组中的下标。矩阵的转置其实就是数组中元素的移动,具体的移动过程如下图:

我们发现,这些移动的元素的下标是一个个环,下标1的元素移动到4,下标4的元素移动到2,下标2的元素移动到1。在编写程序的时候,我们需要解决两个问题:第一个是如何判定环是否重复(已处理过);第二个是如何计算当前元素下标的前驱与后继。
第一个问题:如何判断环是重复已处理过的?因为我们遍历整个数组时下标是从小到大的,所以如果是第一次遍历该环,则第一个下标肯定是这个环中最小的。如果一个环被处理过,那么总能找到一个它的后继是小于它的。从上图可以明显看出来。
第二个问题:如何计算当前元素下标的前驱与后继?假设转置前某个元素的数组下标为i,则它所在行列为(i/N, i%N),转置后所在行列则为(i%N, i/N),可计算转置后数组下标为(i%N)*M+i/N,此为i的后继。假设转置后某个元素的数组下标为i,则它所在行列为(i/M, i%M),则转置前所在行列为(i%M, i/M),可计算此时下标为(i%M)*N+i/M,此为i的前驱。
三、代码实现如下:
/************************************************************************* > File Name: matrix_transpose.cpp > Author: SongLee ************************************************************************/ #include<iostream> using namespace std; /* 后继 */ int getNext(int i, int m, int n) { return (i%n)*m + i/n; } /* 前驱 */ int getPre(int i, int m, int n) { return (i%m)*n + i/m; } /* 处理以下标i为起点的环 */ void movedata(int *mtx, int i, int m, int n) { int temp = mtx[i]; // 暂存 int cur = i; // 当前下标 int pre = getPre(cur, m, n); while(pre != i) { mtx[cur] = mtx[pre]; cur = pre; pre = getPre(cur, m, n); } mtx[cur] = temp; } /* 转置,即循环处理所有环 */ void transpose(int *mtx, int m, int n) { for(int i=0; i<m*n; ++i) { int next = getNext(i, m, n); while(next > i) // 若存在后继小于i说明重复 next = getNext(next, m, n); if(next == i) // 处理当前环 movedata(mtx, i, m, n); } } /* 输出矩阵 */ void print(int *mtx, int m, int n) { for(int i=0; i<m*n; ++i) { if((i+1)%n == 0) cout << mtx[i] << "\n"; else cout << mtx[i] << " "; } } /* 测试 */ int main() { int matrix[4*2] = {1,2,3,4,5,6,7,8}; cout << "Before matrix transposition:" << endl; print(matrix, 4, 2); transpose(matrix, 4, 2); cout << "After matrix transposition:" << endl; print(matrix, 2, 4); return 0; }
运行结果如下图所示:
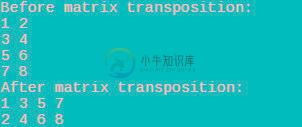
-
矩阵(包括稀疏矩阵)的转置,即互换矩阵中所有元素的行标和列标,如图 1 所示: 图 1 矩阵转置示意图 但如果想通过程序实现矩阵的转置,互换行标和列标只是第一步。因为实现矩阵转置的前提是将矩阵存储起来, 数据结构中提供了 3 种存储矩阵的结构,分别是三元组 顺序表、行逻辑链接的顺序表和十字 链表。如果采用前两种结构,矩阵的转置过程会涉及三元组表也跟着改变的问题,如图 2 所示: 图 2 三元组表的
-
本文向大家介绍Ruby实现的矩阵连乘算法,包括了Ruby实现的矩阵连乘算法的使用技巧和注意事项,需要的朋友参考一下 动态规划解决矩阵连乘问题,随机产生矩阵序列,输出形如((A1(A2A3))(A4A5))的结果。 代码:
-
本文向大家介绍java实现任意矩阵Strassen算法,包括了java实现任意矩阵Strassen算法的使用技巧和注意事项,需要的朋友参考一下 本例输入为两个任意尺寸的矩阵m * n, n * m,输出为两个矩阵的乘积。计算任意尺寸矩阵相乘时,使用了Strassen算法。程序为自编,经过测试,请放心使用。基本算法是: 1.对于方阵(正方形矩阵),找到最大的l, 使得l = 2 ^ k, k为整数并
-
本文向大家介绍C语言实现稀疏矩阵,包括了C语言实现稀疏矩阵的使用技巧和注意事项,需要的朋友参考一下 本文实例为大家分享了C语言实现稀疏矩阵的具体代码,供大家参考,具体内容如下 效果图: 以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持呐喊教程。
-
本文向大家介绍C语言实现矩阵翻转(上下翻转、左右翻转),包括了C语言实现矩阵翻转(上下翻转、左右翻转)的使用技巧和注意事项,需要的朋友参考一下 C语言实现矩阵翻转 上下翻转与左右翻转 实例代码: 动态分配内存 感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!
-
问题内容: 我正在自学一些Java,并且坚持创建2D数组,该数组使用随机值对其进行初始化,然后创建该数组的转置。 示例输出为: 原始矩阵 转置矩阵 ^应该是最终输出。代码的一些帮助将不胜感激! 如果行或列的数量超出指定范围,我想编写代码以生成错误消息。以及是否从命令行读取矩阵元素而不是随机生成它们。 问题答案: 这是返回转置矩阵的int [] []的简单方法… 比起打印二维矩阵,您可以使用如下方法

