《算法题》专题
-
AdaGrad算法
在之前介绍过的优化算法中,目标函数自变量的每一个元素在相同时间步都使用同一个学习率来自我迭代。举个例子,假设目标函数为$f$,自变量为一个二维向量$[x_1, x_2]^\top$,该向量中每一个元素在迭代时都使用相同的学习率。例如,在学习率为$\eta$的梯度下降中,元素$x_1$和$x_2$都使用相同的学习率$\eta$来自我迭代: $$x_1 \leftarrow x_1 - \eta \f
-
9.11 算法
当你编写一个针对一类问题的通用解法,而非针对某一个问题的特定解法时,你就写出了一个算法。我在第一章提到过这个词,但是没有给出详细定义。这也不太好定义,所以我会试用多种方式进行定义。 首先,考虑一些不是算法的问题。当你学习个位数乘法时,你可能会背乘法表。实际上你记住的是100个特定解法,这种知识并不是真正意义的算法。 但是,如果你很“懒”,你可能学习一些作弊技巧。比如,求n与9的乘积,你可以在第一位
-
10 算法
算法策略 分治法T(n)=O(nlogn) 将问题分解成规模较小、相互独立的子问题,各个击破,分而治之。 归并排序 将数列分为几个序列片段,逐趟两两归并,到底层归并成有序数列 最大子段和问题 动态规划法T(n)=O(nW) 将问题分解成互不独立子问题,保存子问题解,需要时再用,例如多项式时间算法 0/1背包问题 LCS最长公共子序列 贪心/贪婪法T(n)=O(n) 不从整体最优考虑,只根据当前信息
-
LRU 算法
一、前言 上一章《Memcached源码分析 - Memcached源码分析之增删改查操作(5) 》中,我们讲到了SET命令的操作。当客户端向Memcached服务端SET一条缓存数据的时候,会将生成的Item地址挂到LRU的链表结构上。这一章节,我们主要讲一下Memcached是如何使用LRU算法的。 LRU:是Least Recently Used 近期最少使用算法。 二、Memcached的
-
1.-算法
名称 原理 复杂度 插入排序 对于元素索引i(i>=1),从头开始,若能找到比 a[i] 大对元素 a[j],则记录 a[i] 的值,将索引 j~i-1 的元素向后移动一位,使用 a[i] 替换 a[j]。优化思路:针对数组可以采用二分查找找到当前元素的插入位置,链表不需要位移操作。 O(n^2/2) 选择排序 从当前元素开始遍历,记录最小值的索引,根据索引交换当前值的最小值,选择排序每次选出最小
-
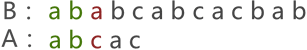 BF算法(串模式匹配算法)
BF算法(串模式匹配算法)主要内容:BF算法原理,BF算法实现,BF算法时间复杂度,总结串的模式匹配算法,通俗地理解,是一种用来判断两个串之间是否具有"主串与子串"关系的算法。 主串与子串:如果串 A(如 "shujujiegou")中包含有串 B(如 "ju"),则称串 A 为主串,串 B 为子串。主串与子串之间的关系可简单理解为一个串 "包含" 另一个串的关系。 实现串的模式匹配的算法主要有以下两种: 普通的模式匹配算法; 快速模式匹配算法; 本节,先来学习 普通模式匹配(BF)
-
数据结构与算法 - KMP算法
KMP算法解决的问题是字符匹配,这个算法把字符匹配的时间复杂度缩小到O(m+n),而空间复杂度也只有O(m),n是target的长度,m是pattern的长度。 部分匹配表(Next数组):表的作用是 让算法无需多次匹配S中的任何字符。能够实现线性时间搜索的关键是 在不错过任何潜在匹配的情况下,我们”预搜索”这个模式串本身并将其译成一个包含所有可能失配的位置对应可以绕过最多无效字符的列表。 Nex
-
算法项目问题
要求你写一份关于以下算法问题的报告:这道题要求你在一组真币中找出一个假币。这枚假硬币之所以能被找到,是因为它和其余的真硬币的重量不一样。不是轻了就是重了,只是你事先不知道。你要做决定的唯一方法是一个经典的带有两个托盘的天平秤。你可以把一个或多个硬币放在一个托盘上,一个相似的数字放在另一个托盘上,并确定哪个托盘有较轻的一堆。例如,如果你只有三个硬币,那么拿硬币1和硬币2称重。如果天平平衡,那么硬币3
-
 20220814大疆算法题
20220814大疆算法题B卷。 题目描述:给定一组任务,每个任务有一个价值value,一个起始时间start,一个结束时间end。对给定的这组任务按照时间依次执行,两任务之间不能有时间重叠。请输出能得到的最大价值,对应所要执行任务的下标。 输入描述:第一行为任务的数量n,接下来n行,每行为一个任务的价值、起始时间和结束时间。如示例1中有8个任务,第一个任务价值为3,起始时间为0,结束时间为6. 输出描述:输出所执行任务的
-
算法题 - 后缀树
后缀树 1.1、后缀树的定义 后缀树(Suffix tree)是一种数据结构,能快速解决很多关于字符串的问题。后缀树的概念最早由Weiner 于1973年提出,既而由McCreight 在1976年和Ukkonen在1992年和1995年加以改进完善。 后缀,顾名思义,就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1…
-
专题-优化算法
Reference 【必读】An overview of gradient descent optimization algorithms - Sebastian Ruder 梯度下降 ../数学/梯度下降法 梯度下降是一种优化算法,通过迭代的方式寻找模型的最优参数; 所谓最优参数指的是使目标函数达到最小值时的参数; 当目标函数是凸函数时,梯度下降的解是全局最优解;但在一般情况下,梯度下降无法保证
-
 讯飞算法三题
讯飞算法三题public static void main(String[] args) { Scanner in = new Scanner(System.in); in.useDelimiter(" "); int n = in.nextInt(); String arrStr = in.next(); String[] ar
-
 360笔试算法题
360笔试算法题1. 传染病防控 并查集,两两判断曼哈顿距离,如果小于k,就将父节点大的点添加到父节点小的点的集合中,统计每个节点集合中的节点个数,返回最大值。 2.盘古开天 线性dp分别求出每个下标作为开始和结束的最长递增序列的长度保存在数组dp1和dp2中。然后遍历判断修改每个下标的高度能得到的最长递增序列的最大值,特别注意如果当前下标(i)的后一个下标(i+1)的高度比当前下标前一个下标(i-1)的高度大于
-
 360二面算法题
360二面算法题今日面了360,面试官说通过了,其他问题都比较常规,但算法题有点意思。 1.假设一个人物的战斗力是5,只能挑战1~5的关卡,超过5就会死掉,不能再战斗。现在给两个战斗力n的人物,给一个用最小挑战次数确定n的算法。 2.大数的排重和排序,输出今日收发过消息的qq号。 问题1我最开始想到的是二分查找,但有可能无法找到结果。第二想到的是按区间查找,例如第一个人物的步长是10,第二个人物的步长是1。 面试
-
数据结构与算法 - 递归算法
从前有座山 山里有座庙 庙里有个老和尚和小和尚 老和尚对小和尚说: 从前有座山 返回1 从前有座山,山里有个庙,庙里有个和尚讲故事……这是一个古老的童谣,每个人都知道下面一句说了什么,但还要不厌其烦的说下去。犹如我们的人性,陷入一种循环,不可逃脱,无法自拔。 所以在我们现实生活中,很多时候也有所谓的重复性,而这种重复性用计算机解决的话,就能够省很多事情。 如果用一部电影来类比的话,那《盗梦空间》就
