《算法题》专题
-
数据结构与算法 - 排序算法
常见排序算法 稳定排序: 冒泡排序 — O(n²) 插入排序 — O(n²) 桶排序 — O(n); 需要 O(k) 额外空间 归并排序 — O(nlogn); 需要 O(n) 额外空间 二叉排序树排序 — O(n log n) 期望时间; O(n²)最坏时间; 需要 O(n) 额外空间 基数排序 — O(n·k); 需要 O(n) 额外空间 不稳定排序 选择排序 — O(n²) 希尔排序 — O
-
数据结构与算法 - 查找算法
ASL 由于查找算法的主要运算是关键字的比较,所以通常把查找过程中对关键字的平均比较次数(平均查找长度)作为衡量一个查找算法效率的标准。ASL= ∑(n,i=1) Pi*Ci,其中n为元素个数,Pi是查找第i个元素的概率,一般为Pi=1/n,Ci是找到第i个元素所需比较的次数。 顺序查找 原理是让关键字与队列中的数从最后一个开始逐个比较,直到找出与给定关键字相同的数为止,它的缺点是效率低下。时间复
-
K-Means 聚类算法 kmeans 聚类算法
算法介绍 K-Means又名为K均值算法,他是一个聚类算法,这里的K就是聚簇中心的个数,代表数据中存在多少数据簇。K-Means在聚类算法中算是非常简单的一个算法了。有点类似于KNN算法,都用到了距离矢量度量,用欧式距离作为小分类的标准。 算法步骤 (1)、设定数字k,从n个初始数据中随机的设置k个点为聚类中心点。 (2)、针对n个点的每个数据点,遍历计算到k个聚类中心点的距离,最后按照离哪个中心
-
SVM 支持向量机算法 Svm 算法
参考资料:http://www.cppblog.com/sunrise/archive/2012/08/06/186474.html http://blog.csdn.net/sunanger_wang/article/details/7887218 我的数据挖掘算法代码:https://github.com/linyiqun/DataMiningAlg
-
最小加法——算法
我在网上遇到了这个问题。 给定一个整数:N和一个数组int arr[],您必须向数组中添加一些元素,以便可以使用(添加)数组中的元素从1生成到N。 请记住,在生成某个x(1)时,只能使用数组中的每个元素一次 有人能给点提示吗?
-
对数算法
问题内容: 我需要以任何精度评估任何底数的对数。是否有一种算法?我使用Java编程,所以我对Java代码很好。 问题答案: 使用此身份: log b(n)= log e(n)/ log e(b) 其中可以在任何一个基对数函数,是数量和是基础。例如,在Java中,这将找到以2为底的对数256: 顺便使用base 。还有使用base的。
-
分区算法
操作系统实现了各种算法,以便找出链表中的空洞并将它们分配给进程。 关于每种算法的解释如下。 1. 第一拟合算法 第一拟合算法(First Fit)算法扫描链表,每当它找到第一个足够大的孔来存储进程时,它就会停止扫描并将进程加载到该进程中。 该过程产生两个分区。 其中,一个分区将是一个空洞,而另一个分区将存储该进程。 First Fit算法按照起始索引的递增顺序维护链表。这是所有算法中最简单的实现方
-
寻路算法
主要内容:src/runoob/graph/Path.java 文件代码:图的寻路算法也可以通过深度优先遍历 dfs 实现,寻找图 graph 从起始 s 点到其他点的路径,在上一小节的实现类中添加全局变量 from数组记录路径,from[i] 表示查找的路径上i的上一个节点。 首先构造函数初始化寻路算法的初始条件,from = new int[G.V()] 和 from = new int[G.V()],并在循环中设置默认值,visited 数组全部为false,fr
-
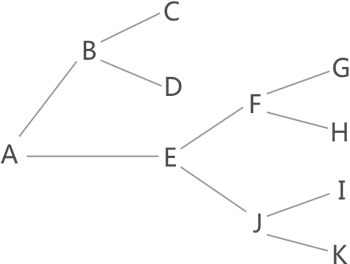 回溯算法
回溯算法主要内容:回溯算法的应用场景在图 1 中找到从 A 到 K 的行走路线,一些读者会想到用穷举算法(简称穷举法),即简单粗暴地将从 A 出发的所有路线罗列出来,然后逐一筛选,最终找到正确的路线。 图 1 找从A到K的行走路线 图 1 中,从 A 出发的路线有以下几条: A-B-C A-B-D A-E-F-G A-E-F-H A-E-J-I A-E-J-K 穷举法会一一筛选这些路线,最终找到 A-E-J-K 。 本节要讲的回溯算
-
贪心算法
主要内容:贪心算法的实际应用《 算法是什么》一节讲到,算法规定了解决问题的具体步骤,即先做什么、再做什么、最后做什么。贪心算法是所有算法中最简单,最易实现的算法,该算法之所以“贪心”,是因为算法中的每一步都追求最优的解决方案。 举个例子,假设有 1、2、5、10 这 4 种面值的纸币,要求在不限制各种纸币使用数量的情况下,用尽可能少的纸币拼凑出的总面值为 18。贪心算法的解决方案如下: 率先选择一张面值为 10 的纸币,可以
-
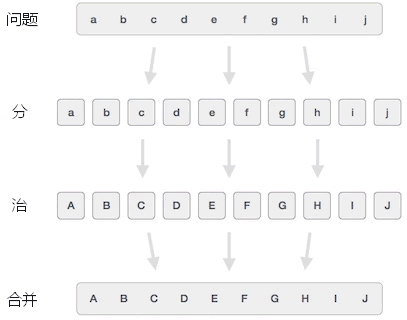 分治算法
分治算法主要内容:分治算法的利弊,分治算法的应用场景实际场景中,我们之所以觉得有些问题很难解决,主要原因是该问题涉及到大量的数据,如果只需要处理少量的数据,问题会变得非常容易解决。 举一个简单的例子,设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说,直接实现对 1000 个整数进行排序是非常困难的。而同样的问题,如果转换成对 2 个整数进行排序,解决起来就很容易。 分治算法中,“分治”即“分而治之”的意思。分治算法
-
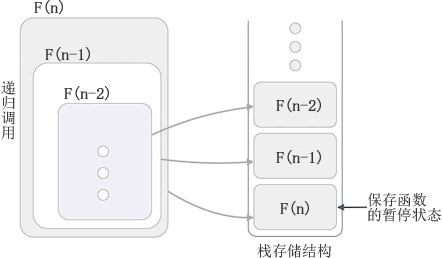 递归算法
递归算法主要内容:递归的底层实现机制编程语言中,我们习惯将函数(方法)调用自身的过程称为 递归,调用自身的函数称为 递归函数,用递归方式解决问题的算法称为 递归算法。 函数(方法)调用自身的实现方式有 2 种,分别是: 1) 直接调用自身,例如: 2) 间接调用自身,例如: 程序中,function1() 函数内部调用了 function2() 函数,而 function2() 函数内部又调用了 function1() 函数。也就是
-
 回溯算法
回溯算法主要内容:回溯VS递归,回溯算法的实现过程回溯算法,又称为 “试探法”。解决问题时,每进行一步,都是抱着试试看的态度,如果发现当前选择并不是最好的,或者这么走下去肯定达不到目标,立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。 例如,在解决列举集合 {1,2,3} 中所有子集的问题中,就可以使用回溯算法。从集合的开头元素开始,对每个元素都有两种选择:取还是舍。当确定了一个元素的取舍之后,再进行下一个元素,直到集合最后一个元
-
投弹算法
我有一个由非负整数组成的矩阵。例如: “投下炸弹”将目标单元及其所有八个相邻单元的数量减少一个,至少为零。 确定将所有单元减少到零所需的最小炸弹数量的算法是什么? B选项(由于我不是一个细心的读者) 事实上,这个问题的第一个版本并不是我要寻找的答案。我没有仔细阅读整个任务,还有其他限制,让我们说: 那么简单的问题呢,当行中的序列必须是非递增的: 是可能的输入序列 不可能,因为7- 也许为“更容易”
-
高耸算法
问题内容: 在《破解编码面试》第四版中,存在这样的问题: 马戏团正在设计一个塔楼套路,由站在一个人的肩膀上的人组成。出于实际和美学的原因,每个人都必须比其下方的人矮一些和矮一些。考虑到马戏团中每个人的身高和体重,编写一种方法来计算此类塔楼中的最大人数。 示例:输入(ht,wt):(65,100)(70,150)(56,90)(75,190)(60,95)(68,110) 输出:最长的塔长为6,从上
