《haskell》专题

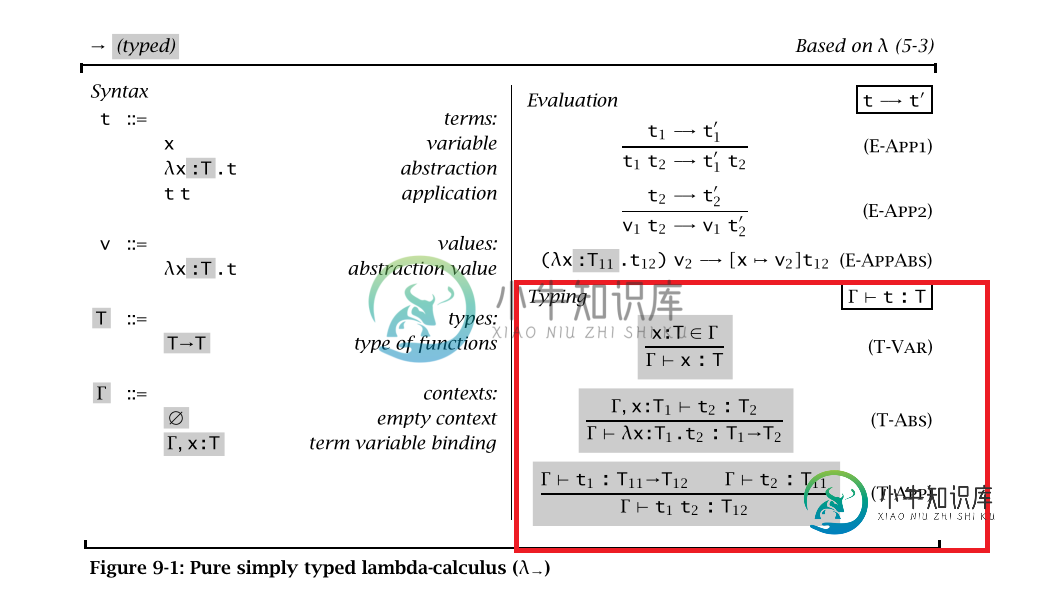
我在Haskell编程中的冒险并不都是史诗般的。我正在实现简单的Lambda演算，我很高兴完成了、以及，希望它们是正确的。剩下的是，就像红色框中定义的那样（在下图中），我正在为此寻找指导。 如果我说错了请指正， （1）但是我发现返回给定变量的类型。Haskell中的什么构造返回？我知道在中是，但我正在寻找一个在下工作的。 （3）对于（T-APP）和（T-ABS)，我假设我分别对和应用程序应用了替换

部分答案可能来自领域理论。如果我理解正确的话，的元素并不全是集合论函数（根据康托定理，这些函数比大），而只是连续函数。如果是，定义这种连续性的拓扑是什么？为什么类型的Haskell术语对它是连续的？

从范畴理论的角度来看，这个答案包括以下陈述： ...事实是co和逆变函子之间没有真正的区别，因为每个函子都是协变函子。 更详细地说，从C类到D类的逆变函子F无非是F型的（协变）函子:COP→D，从C的相反类到D类。 另一方面，Haskell的和仅要求分别为实例定义和。这表明，从Haskell的角度来看，存在但不是的对象（反之亦然）。 因此，在范畴理论中，似乎“co和逆变函子之间没有真正的区别”，而

在那个网站上，我读到Haskell前奏曲中的函数类型实际上是一个内函数。（以上类别中的c类和d类均为Hask） 通读了这一页后，我在想。如果Haskell使用实函数而不仅仅是内函数，它是否更适合于元编程？ 假设我们有以下内容（Js代表Javascript）

在Haskell中有Hask，其中的对象是Haskell类型，而态性是Haskell函数。但是，type类有一个函数，它在这些类型（因此是对象而不是类别本身）之间进行映射： 和都是HASK中的对象。这是否意味着Haskell中的每个实例都是一个内函数，如果不是，真的表示一个函数吗？

现在考虑一个成员类型为的typeclass。例如，可以想象一个类型类，它对应于组的类别（从技术上讲，是的子类别，其对象包含Haskell的所有类型）。概括： 问题2:Haskell中每个成员类型为的typeclass是否都对应于某个类别（从技术上讲:的某个子类别）？ 由此可以提出下一个一般性问题： 一般问题：每一个Haskell类型类是否都对应于某种范畴理论的概念？ Edit：至少，您可以说，由于

我正在研究λ-演算的最佳实现。有一个特殊的lambda项子集非常有效。它对应于具有不动点的初等仿射逻辑的类型系统。为了测试我对该算法的实现，我必须在该系统上编写适度复杂的术语。如果没有基础设施，这是很难的。我必须使用非类型化的lambda演算，然后手动添加类型；没有检查，统一，没有类型错误。

对于特定的任务，我需要在可变数组中进行大量快速、单独的写操作。为了检查性能，我使用了以下测试：

由于没有快速的lambda计算器，我使用上面的策略将非类型化lambda演算的术语编译为Haskell，以便快速计算它们。我对它的性能印象深刻：该程序创建了一个从到的数字列表，并在我的计算机上在不到一秒钟的时间内将它们相加。这比我预期的要快得多--只比Haskell直接等价物慢4倍--并且足以对我的目标有用。但是，请注意，为了满足类型系统的需要，我必须将函数和术语包装在fun/num构造函数下面。

假设一个纯λ函数是一个除了抽象和应用之外什么都没有的术语。在JavaScript上，通过对收集参数列表的各种函数应用所有抽象，可以推断出纯函数的源代码。也就是说，这是可能的： 关于这个要点，请参见lambdaSource的代码。这个函数对我的兴趣特别有用，因为它允许我使用现有的JS引擎规范非类型化的lambda演算表达式，比我自己编写的任何简单的计算器都快得多。此外，我知道λ-微积分函数可以在的帮

其中是用于定义替换的函数。 然而，当我试图使用beta约简来约简表达式时，我得到了一个非穷举模式错误，我不明白为什么。我能做的修复它是在底部添加一个额外的大小写，如下所示： 但是，如果我这样做了，那么lambda表达式根本不会被缩减，这意味着函数的输入和输出是相同的。 如果使用第一个函数而不添加最后一个大小写，则为非穷尽模式 或完全相同的表达式App(ABS1(ABS2(VAR1)))(VAR3)

我现在被困在实现“alpha-同余”（在一些教科书中也被称为“alpha-等价”或“alpha-相等”）上。我希望能够检查两个λ表达式是否相等。例如，如果我在解释器中输入以下表达式，它应该得到True(用于指示lambda符号）： 问题在于理解下列λ表达式是否被认为是alpha等价的： 在的情况下，我猜答案是。这是因为和，两者的右侧是相等的（其中符号用于表示alpha缩减）。 简而言之，如何实现函

Haskell中的Zippers是一个指向数据结构(例如树)的某些特定位置的指针。 假设具有5个元素的树，可以将其表示为完全二叉树。如果要更新此列表的最后一个元素，则需要遍历所有元素以到达最后一个元素，然后再进行更新。 但是，如果我们以具有N个元素的树是的集合的方式构造树，那该怎么办？ 那么，可以不需要遍历所有不需要的(N-1)个元素。直接更新第N个元素，这正是Zipper的概念。它聚焦或指向树的

单子(Monad)只是一种带有某些附加功能的Applicative Functor。它是一个类，它管理三个基本规则(称为一元规则)。 这三个规则严格适用于Monad声明，如下所示： 单子(Monad)式声明的三个基本原则是： 左标识定律 - 返回函数不会更改值，并且不应更改Monad中的任何内容。可以表示为：； 右标识定律 - 返回函数不会改变值，也不会改变Monad中的任何内容。它可以表示为：；