Haskell用于Lambda演算，类型推断

Question

我在Haskell编程中的冒险并不都是史诗般的。我正在实现简单的Lambda演算，我很高兴完成了语法、求值以及替换，希望它们是正确的。剩下的是键入，就像红色框中定义的那样（在下图中），我正在为此寻找指导。

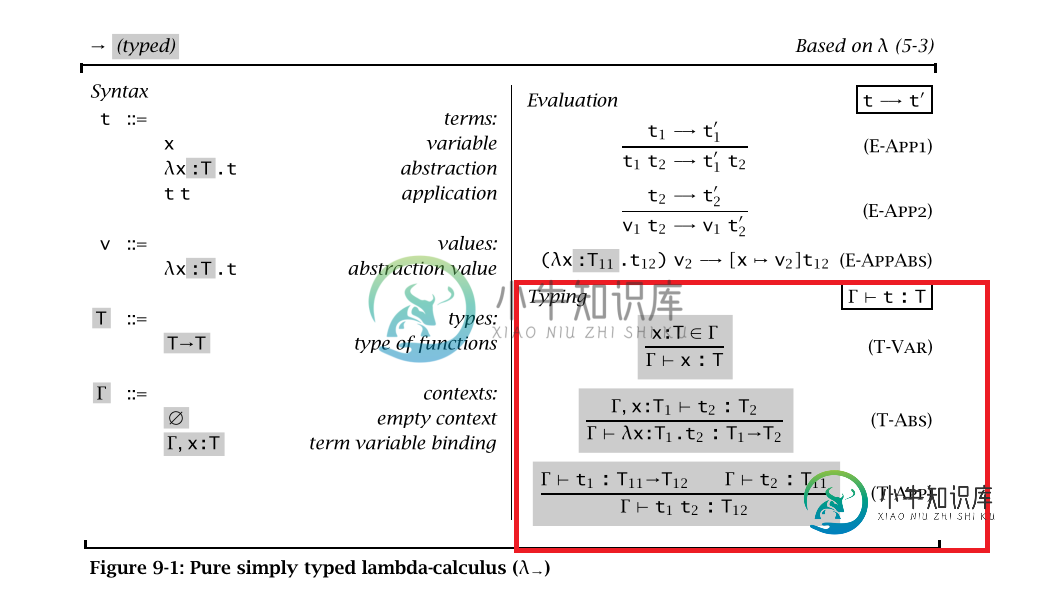
如果我说错了请指正，

（1）但是我发现(T-Var)返回给定变量X的类型。Haskell中的什么构造返回type？我知道在prelude中是:tx，但我正在寻找一个在main=do下工作的。

（3）对于（T-APP）和（T-ABS)，我假设我分别对抽象字符串Lambda和应用程序lambdalambda应用程序应用了替换。缩减窗体的类型是返回的类型。那是正确的吗？

提前谢谢...

Answer 1

从简单类型化的lambda演算中得到的关键是，类型是在lambda绑定器本身上注释的，每个lambda术语都有一个类型。Pierce提供的键入规则是如何机械地键入检查表达式是否键入良好。类型推断是他在这本书后面讨论的一个主题，这是从非类型化表达式中恢复类型。

除此之外，Pierce在这个例子中没有给出一些基本类型(bool、int)，它们在实现算法时很有帮助，所以我们将把它们附加到定义中。

t = x
  | λ x : T . t
  | t t
  | <num>
  | true
  | false

T = T -> T
  | TInt
  | TBool

如果我们把它翻译成Haskell，我们会得到：

type Sym = String

data Expr
    = Var Sym
    | Lam Sym Type Expr
    | App Expr Expr
    | Lit Ground
     deriving (Show, Eq, Ord)

data Ground = LInt Int
            | LBool Bool
            deriving (Show, Eq, Ord)

data Type = TInt
          | TBool
          | TArr Type Type
          deriving (Eq, Read, Show)

type Env = [(Sym, Type)]

extend :: Env -> (Sym, Type) -> Env
extend env xt = xt : env

data TypeError = Err String deriving Show

instance Error TypeError where
    noMsg = Err ""

type Check a = ErrorT TypeError Identity a

check :: Env -> Expr -> Check Type
check _ (Lit LInt{}) = return TInt
check _ (Lit LBool{}) = return TBool

--  x : T ∈ Γ
--  ----------
--  Γ ⊦ x : T

check env (Var x) = case (lookup x env) of
    Just e  -> return e
    Nothing -> throwError $ Err "Not in Scope"

--  Γ, x : T ⊦ e : T'
--  --------------------
--  Γ ⊦ λ x . e : T → T'

check env (Lam x t e) = do
  rhs <- (check (extend env (x,t)) e)
  return (TArr t rhs)

--  Γ ⊦ e1 : T → T'   Γ ⊦ e2 : T
--  ----------------------------
--  Γ ⊦ e1 e2 : T'

check env (App e1 e2) = do
  t1 <- check env e1
  t2 <- check env e2
  case t1 of
     (TArr t1a t1r) | t1a == t2 -> return t1r
     (TArr t1a _) -> throwError $ Err "Type mismatch"
     ty -> throwError $ Err "Trying to apply non-function"

runCheck :: Check a -> Either TypeError a
runCheck = runIdentity . runErrorT

checkExpr :: Expr -> Either TypeError Type
checkExpr x = runCheck $ check [] x

当我们对表达式调用checkexpr时，我们要么返回表达式的有效类型，要么返回typeerror来指示函数的错误。

例如，如果我们有一个术语：

(λx : Int -> Int . x) (λy : Int. y) 3
App (App (Lam "x" (TArr TInt TInt) (Var "x")) (Lam "y" TInt (Var "y"))) (Lit (LInt 3))

我们希望我们的类型检查器验证它是否具有输出类型tint。

(λx : Int -> Int . x) 3
App (Lam "x" (TArr TInt TInt) (Var "x")) (Lit (LInt 3))