《matlab》专题
-
 Matlab多项式
Matlab多项式主要内容:评估计算多项式,计算多项式的根,多项式曲线拟合MATLAB表示多项式为包含由下降幂排列的系数的行向量。 例如,方程式 可以表示为 - 评估计算多项式 多值函数用于评估计算指定值的多项式。 例如,要评估前面的多项式,在,可使用以下代码 - MATLAB执行上述语句返回以下结果 - MATLAB还提供函数用于评估矩阵多项式。 矩阵多项式是以矩阵为变量的多项式。 例如,下面创建一个方阵并评估求值多项式,在 - MATLAB执行上述代码语句返回以下结
-
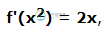 Matlab整合集成
Matlab整合集成主要内容:使用MATLAB找到不确定的积分,使用MATLAB查找定积分整合(或也叫作集成)涉及两种本质上不同类型的问题。 第一种类型问题是给出了函数的导数,并且想要找到该函数。所以基本上扭转了差异化的过程。 这种反向过程被称为抗分化,或者找到原始函数,或者找到不确定的积分。 第二种类型问题是涉及相当多的非常小的数量,然后随着数量的大小接近于零,而术语的数量趋向于无穷大。这个过程导致了定积分的定义。 确定的积分用于查找区域,体积,重心,转动惯量,由力完成的工作以及许多
-
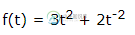 Matlab微分和导数
Matlab微分和导数主要内容:基本微分规则的验证,指数,对数和三角函数的导数,计算高阶导数,查找曲线的最大和最小值,求解微分方程MATLAB提供用于计算符号导数的命令。 以最简单的形式,将要微分的功能传递给命令作为参数。 例如,计算函数的导数的方程式 - 例子 创建脚本文件并在其中键入以下代码 - 执行上面示例代码,得到以下结果 - 以下是使用Octave 计算的写法 - 执行上面示例代码,得到以下结果 - 基本微分规则的验证 下面简要说明微分规则的各种方程或规则,并验证这些规则。 为此,我们将写一个第一阶导数和二
-
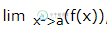 Matlab微积分
Matlab微积分主要内容:计算极限,使用Octave计算极限,验证极限的基本属性,使用Octave验证极限的基本属性,左右边界极限MATLAB提供了解决微分和积分微积分的各种方法,求解任何程度的微分方程和极限计算。可以轻松绘制复杂功能的图形,并通过求解原始功能以及其衍生来检查图形上的最大值,最小值和其他固定点。 本章将介绍微积分问题。在本章中,将讨论预演算法,即计算功能限制和验证限制属性。 在下一章微分中,将计表达式的导数,并找到一个图的局部最大值和最小值。我们还将讨论求解微分方程。 最后,在“整合/集成”一章
-
Matlab代数(方程求解)
主要内容:在MATLAB中求解基本代数方程,求解代数中的基本代数方程,在MATLAB中求解二次方程,在Octave中求解二次方程,求解MATLAB中的高阶方程,在Octave中求解高阶方程,MATLAB中求解方程组,在Octave中求解方程组,在MATLAB中扩展和集合方程,在Octave扩展和集合方程,代数表达式的因式分解和简化到目前为止,我们已经看到所有的例子都在MATLAB以及它的GNU,或者称为Octave。 但是,为了求解基本代数方程,MATLAB和Octave都不同,所以这里将分别介
-
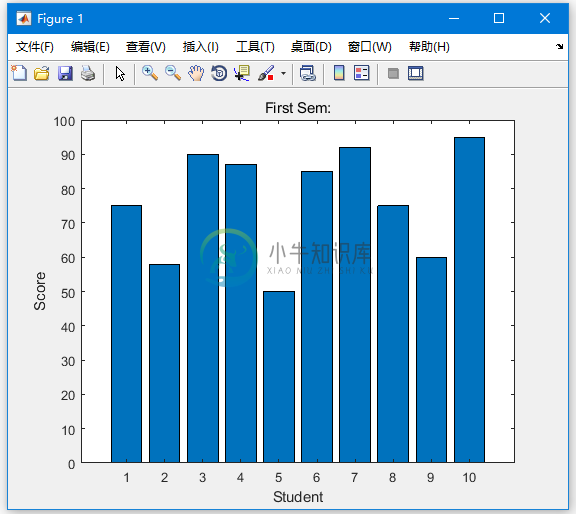 Matlab图形
Matlab图形主要内容:绘制条形图,绘制等高线,三维图本章将继续探讨MATLAB的绘图和图形函数功能。下面将会讨论 - 绘制条形图 绘制轮廓 三维图 绘制条形图 命令绘制二维条形图,下面举个例子来演示如何使用。 示例 假设有名学生,这些学生某次考试获得分数是:75,58,90,87,50,85,92,75,60和95,使用这此分数来绘制条形图如下。 创建脚本文件并键入以下代码 - 运行文件时,MATLAB显示以下条形图 - 绘制等高线 两个变量的函数
-
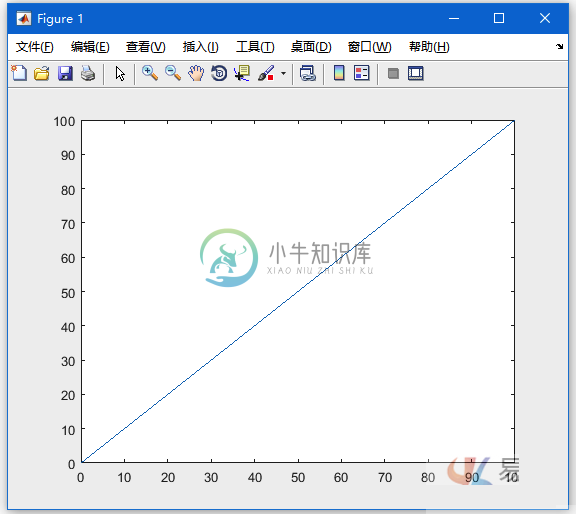 Matlab绘图
Matlab绘图主要内容:在图上添加标题,标签,网格线和缩放,在同一个图上绘制多个函数,在图上设置颜色,设置轴刻度,生成子图要使用函数来绘制图形,需要执行以下步骤: 通过指定要绘制函数的变量的值的范围来定义。 定义函数, 调用命令,如下: 以下示例将演示该概念。下面绘制的值范围是从到,使用简单函数,增量值为。 创建脚本文件并键入以下代码 - 执行上面示例代码,得到以下结果 - 下面再来一个例子来绘制函数。 在这个例子中,将绘制两个具有相同函数的图,但是在第二次,将减小增量的值。请注意,当减少增量时,图形变得更平
-
Matlab数据导出
主要内容:示例,写到日记文件,将数据导出到具有低级I/O的文本数据文件MATLAB中的数据导出(或输出)可以理解为写入文件。 MATLAB允许在其他应用程序中使用读取ASCII文件的数据。 为此,MATLAB提供了几个数据导出选项。 可以创建以下类型的文件: 来自数组的矩形,有分隔符的ASCII数据文件。 日记(或日志)文件的按键和结果文本输出。 使用等低级函数的专用ASCII文件。 MEX文件访问写入特定文本文件格式的C/C++或Fortran例程。 除此之外,还
-
 Matlab数据导入
Matlab数据导入主要内容:示例 - 1,示例 - 2,示例 - 3,低级文件I/O,导入具有低级别I/O的文本数据文件,示例在MATLAB中导入数据意味着从外部文件加载数据。importdata函数允许加载不同格式的各种数据文件。它有以下五种形式 - 序号 函数 描述 1 从文件filename中将数据加载到数组A中。 2 从系统剪贴板而不是从文件加载数据。 3 解析作为在文件,文件名或剪贴板数据中的列分隔符。可以使用与上述语法中的任何输入参数。 4 从ASCII文件,文件名或剪贴板加载数据,从行头标题开始读取
-
Matlab函数
主要内容:示例,匿名函数,主函数和次函数,示例,嵌套函数,私有函数,示例,全局变量一个函数是一组在一起执行任务的语句。 在MATLAB中,函数在单独的文件中定义。文件的名称和函数的名称应该是一样的。 函数在自己的工作空间内的变量上运行,这个变量也称为本地工作空间,与在MATLAB命令提示符下访问的工作区(称为基本工作区)不同。 函数可以接受多个输入参数,并可能返回多个输出参数。 函数语句的语法是 - 示例 以下名称为的函数应写入名称为的文件中。它需要五个数字作为参数,并返回参数
-
Matlab字符串
主要内容:矩形字符数组,示例,将字符串组合成单元格数组,示例,MATLAB中的字符串函数,例子在MATLAB中创建一个字符串非常简单。 事实上,在前面的示例中我们已经使用了很多次。 例如,在命令提示符下键入以下内容: MATLAB执行上述语句并返回以下结果 - MATLAB将所有变量视为数组,并将字符串视为字符数组。使用命令来检查上面创建的变量 - 有趣的是,可以使用或等数字转换函数将字符串中的字符转换为数字代码。 函数将整数向量转换回到字符 - 示例 创建脚本文件并在其中键入以下代码 -
-
Matlab数字
主要内容:转换为各种数值数据类型,最小和最大的整数,最小和最大的浮点数,以下是纠正/补充内容:MATLAB支持包括有符号和无符号整数以及单精度和双精度浮点数的各种数字类型。 默认情况下,MATLAB将所有数值存储为双精度浮点数。 可以选择将任何数字或数组的数字存储为整数或单精度数字。 所有数字类型都支持基本的数组运算和数学运算。 转换为各种数值数据类型 MATLAB提供以下函数来将数值转换为各种数字数据类型 - 函数 描述说明 转换为双精度数 转换为单精度数 转换为位有符号整数 转换为位有
-
Matlab冒号符号
主要内容:示例冒号()是MATLAB中最有用的操作符之一。它用于创建向量,下标数组,并为迭代指定。 如果要创建一个包含从到的整数的行向量,则书写为 - MATLAB执行语句并返回一个包含整数的行向量,从到 - 如果要指定一个增量值,例如 - MATLAB执行语句并返回以下结果 - 再来看看一个例子 - MATLAB执行语句并返回以下结果 - 可以使用冒号运算符创建索引向量,以选择数组的行,列或元素。 下表描述了
-
Matlab数组
主要内容:MATLAB中的特殊数组,魔方,多维数组,数组函数,例子,排序数组,单元阵列,访问单元格数组数据MATLAB中所有数据类型的所有变量都是多维数组。向量是一维数组,矩阵是二维数组。 我们前面已经讨论和学习过向量和矩阵。 在本章中,将讨论和学习多维数组。 然而,在此之前,让我们先学习一些特殊类型的数组。 MATLAB中的特殊数组 在本节中,我们将讨论学习一些创建一些特殊数组的函数。对于这些函数,单个参数创建一个正方形数组,双参数创建矩形数组。 函数是用来创建一个全零的数组 - 例如 - 执
-
Matlab矩阵
主要内容:引用矩阵中的元素,删除矩阵中的一行或一列,矩阵运算,以下是纠正/补充内容:矩阵是数字的二维数组。 在MATLAB中,可以通过在每行中输入元素来创建一个矩形,以逗号或空格分隔数字,并使用分号标记每一行的结尾。 例如,创建一个矩阵 - MATLAB将执行上述语句并返回以下结果 - 引用矩阵中的元素 要引用矩阵的第行和第列中的元素,可以这样书写 - 例如,要引用矩阵的第行和第列中的元素,如上一节所述,可以这样书写 - MATLAB执行上述语句并返回以下结果 - 要引用第列中的
