《算法求职》专题

参考资料：http://www.cppblog.com/sunrise/archive/2012/08/06/186474.html                       http://blog.csdn.net/sunanger_wang/article/details/7887218 我的数据挖掘算法代码：https://github.com/linyiqun/DataMiningAlg

第三题丢苹果 题目大意是： 有k个苹果和n层楼，k>=1, n>=1 假设有某层f（0<=f<=n），>f的楼层扔下来苹果会摔碎，<=f仍的苹果不会摔碎 每丢一次苹果算一次测试，如果苹果没摔碎可以在下一次测试时继续使用 问，最少丢几次可以确定f 输入：k,n 输出：最少丢几次 我想用二分法，计算最大二分次数就行了。然后考虑了只剩一个苹果的时候，次数必须+=剩余未判断的最大楼层个数 结果只通过了40

本文向大家介绍Java实现求子数组和的最大值算法示例，包括了Java实现求子数组和的最大值算法示例的使用技巧和注意事项，需要的朋友参考一下 本文实例讲述了Java实现求子数组和的最大值算法。分享给大家供大家参考，具体如下： 一般C和C++在算法实现中使用较多，下面我们通过java语言实现算法，更有亲切感。 题目： 输入一个整形数组，数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组，

本文向大家介绍Java求10到100000之间的水仙花数算法示例，包括了Java求10到100000之间的水仙花数算法示例的使用技巧和注意事项，需要的朋友参考一下 本文实例讲述了Java求10到100000之间的水仙花数算法。分享给大家供大家参考，具体如下： 水仙花数： 概念：水仙花数是指一个 n 位数 ( n≥3 )，它的每个位上的数字的 n 次幂之和等于它本身。(例如:1^3 + 5^3+ 3

我正在使用spring security saml扩展来实现SSO，并将ADF作为IDP。 据我所知，Spring Security使用open saml对SAML请求进行签名，并使用SHA1with RSA作为签名算法。 我们需要更改以使用SHA256withRSA签署SAML请求。 这怎么能做到呢？ 感谢您对此提出的任何建议。提前非常感谢

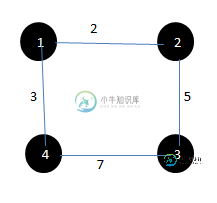
给出加权无向图G（v,e）的权值为w（e）,求出使每对顶点(u,v)∈G连通（简言之为)且所选边的权值范围最小（或最小权值与最大权值之差最小）的边集。 我尝试了贪婪的方法，根据权重对边进行排序，然后在排序的数组中选择连续边之间权重差最小的两条边(G[index=current_left],G[index+1=current_right])，然后根据(current_left,current_lef

问题：“一种计算六位数的算法，其中前三位数的和等于后三位数的和。” 我在一次采访中遇到了这个问题，想知道最好的解决方案。这就是我现在所拥有的。 方法1：暴力解决方案当然是检查每个数字（100000到999999之间）的前三位和后三位的总和是否相等。如果是，则递增某个计数器，该计数器记录所有此类数字。 但这检查了所有900,000个号码，因此效率低下。 方法2：既然我们被问到“有多少”这样的数字，而

我检查了用Kadane算法求最大和的连续子数组的解，我不知道为什么我们在代码中需要全局最大值（下面的代码中是global_max)。 下面是用来查找具有最大和的连续子数组的python代码

我在网上遇到了这个问题。 给定一个整数：N和一个数组int arr[]，您必须向数组中添加一些元素，以便可以使用（添加）数组中的元素从1生成到N。 请记住，在生成某个x（1）时，只能使用数组中的每个元素一次 有人能给点提示吗？

问题内容： 我需要以任何精度评估任何底数的对数。是否有一种算法？我使用Java编程，所以我对Java代码很好。 问题答案： 使用此身份： log b（n）= log e（n）/ log e（b） 其中可以在任何一个基对数函数，是数量和是基础。例如，在Java中，这将找到以2为底的对数256： 顺便使用base 。还有使用base的。

操作系统实现了各种算法，以便找出链表中的空洞并将它们分配给进程。 关于每种算法的解释如下。 1. 第一拟合算法 第一拟合算法(First Fit)算法扫描链表，每当它找到第一个足够大的孔来存储进程时，它就会停止扫描并将进程加载到该进程中。 该过程产生两个分区。 其中，一个分区将是一个空洞，而另一个分区将存储该进程。 First Fit算法按照起始索引的递增顺序维护链表。这是所有算法中最简单的实现方

主要内容：src/runoob/graph/Path.java 文件代码：图的寻路算法也可以通过深度优先遍历 dfs 实现，寻找图 graph 从起始 s 点到其他点的路径，在上一小节的实现类中添加全局变量 from数组记录路径，from[i] 表示查找的路径上i的上一个节点。 首先构造函数初始化寻路算法的初始条件，from = new int[G.V()] 和 from = new int[G.V()]，并在循环中设置默认值，visited 数组全部为false，fr

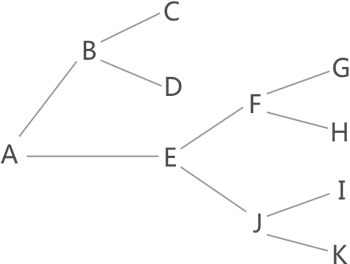
主要内容：回溯算法的应用场景在图 1 中找到从 A 到 K 的行走路线，一些读者会想到用穷举算法（简称穷举法），即简单粗暴地将从 A 出发的所有路线罗列出来，然后逐一筛选，最终找到正确的路线。 图 1 找从A到K的行走路线 图 1 中，从 A 出发的路线有以下几条： A-B-C A-B-D A-E-F-G A-E-F-H A-E-J-I A-E-J-K 穷举法会一一筛选这些路线，最终找到 A-E-J-K 。 本节要讲的回溯算

主要内容：贪心算法的实际应用《 算法是什么》一节讲到，算法规定了解决问题的具体步骤，即先做什么、再做什么、最后做什么。贪心算法是所有算法中最简单，最易实现的算法，该算法之所以“贪心”，是因为算法中的每一步都追求最优的解决方案。 举个例子，假设有 1、2、5、10 这 4 种面值的纸币，要求在不限制各种纸币使用数量的情况下，用尽可能少的纸币拼凑出的总面值为 18。贪心算法的解决方案如下： 率先选择一张面值为 10 的纸币，可以

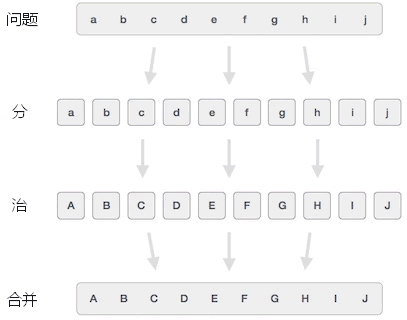
主要内容：分治算法的利弊,分治算法的应用场景实际场景中，我们之所以觉得有些问题很难解决，主要原因是该问题涉及到大量的数据，如果只需要处理少量的数据，问题会变得非常容易解决。 举一个简单的例子，设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说，直接实现对 1000 个整数进行排序是非常困难的。而同样的问题，如果转换成对 2 个整数进行排序，解决起来就很容易。 分治算法中，“分治”即“分而治之”的意思。分治算法