第九章:数字
处理数字是 Common Lisp 的强项之一。Common Lisp 有着丰富的数值类型,而 Common Lisp 操作数字的特性与其他语言比起来更受人喜爱。
9.1 类型 (Types)
Common Lisp 提供了四种不同类型的数字:整数、浮点数、比值与复数。本章所讲述的函数适用于所有类型的数字。有几个不能用在复数的函数会特别说明。
整数写成一串数字:如 2001 。浮点数是可以写成一串包含小数点的数字,如 253.72 ,或是用科学表示法,如 2.5372e2 。比值是写成由整数组成的分数:如 2/3 。而复数 a+bi 写成 #c(a b) ,其中 a 与 b 是任两个类型相同的实数。
谓词 integerp 、 floatp 以及 complexp 针对相应的数字类型返回真。图 9.1 展示了数值类型的层级。
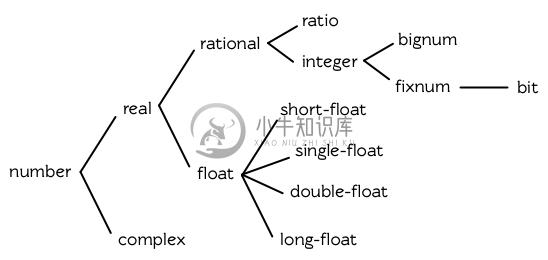
图 9.1: 数值类型
要决定计算过程会返回何种数字,以下是某些通用的经验法则:
- 如果数值函数接受一个或多个浮点数作为参数,则返回值会是浮点数 (或是由浮点数组成的复数)。所以
(+ 1.0 2)求值为3.0,而(+ #c(0 1.0) 2)求值为#c(2.0 1.0)。 - 可约分的比值会被转换成最简分数。所以
(/ 10 2)会返回5。 - 若计算过程中复数的虚部变成
0时,则复数会被转成实数 。所以(+ #c(1 -1) #c(2 1))求值成3。
第二、第三个规则可以在读入参数时直接应用,所以:
> (list (ratiop 2/2) (complexp #c(1 0))) (NIL NIL)
9.2 转换及取出 (Conversion and Extraction)
Lisp 提供四种不同类型的数字的转换及取出位数的函数。函数 float 将任何实数转换成浮点数:
> (mapcar #'float '(1 2/3 .5)) (1.0 0.6666667 0.5)
将数字转成整数未必需要转换,因为它可能牵涉到某些资讯的丧失。函数 truncate 返回任何实数的整数部分:
> (truncate 1.3) 1 0.29999995
第二个返回值 0.29999995 是传入的参数减去第一个返回值。(会有 0.00000005 的误差是因为浮点数的计算本身就不精确。)
函数 floor 与 ceiling 以及 round 也从它们的参数中导出整数。使用 floor 返回小于等于其参数的最大整数,而 ceiling 返回大于或等于其参数的最小整数,我们可以将 mirror? (46 页,译注: 3.11 节)改成可以找出所有回文(palindromes)的版本:
(defun palindrome? (x)
(let ((mid (/ (length x) 2)))
(equal (subseq x 0 (floor mid))
(reverse (subseq x (ceiling mid))))))
和 truncate 一样, floor 与 ceiling 也返回传入参数与第一个返回值的差,作为第二个返回值。
> (floor 1.5) 1 0.5
实际上,我们可以把 truncate 想成是这样定义的:
(defun our-truncate (n)
(if (> n 0)
(floor n)
(ceiling n)))
函数 round 返回最接近其参数的整数。当参数与两个整数的距离相等时, Common Lisp 和很多程序语言一样,不会往上取(round up)整数。而是取最近的偶数:
> (mapcar #'round '(-2.5 -1.5 1.5 2.5)) (-2 -2 2 2)
在某些数值应用中这是好事,因为舍入误差(rounding error)通常会互相抵消。但要是用户期望你的程序将某些值取整数时,你必须自己提供这个功能。 λ
浮点数下溢(underflow)与溢出(overflow),都会被 Common Lisp 视为错误 :
> (* most-positive-long-float 10) Error: floating-point-overflow
9.8 范例:追踪光线 (Example: Ray-Tracing)
作为一个数值应用的范例,本节示范了如何撰写一个光线追踪器 (ray-tracer)。光线追踪是一个高级的 (deluxe)渲染算法: 它产生出逼真的图像,但需要花点时间。
要产生一个 3D 的图像,我们至少需要定义四件事: 一个观测点 (eye)、一个或多个光源、一个由一个或多个平面所组成的模拟世界 (simulated world),以及一个作为通往这个世界的窗户的平面 (图像平面「image plane」)。我们产生出的是模拟世界投影在图像平面区域的图像。
光线追踪独特的地方在于,我们如何找到这个投影: 我们一个一个像素地沿着图像平面走,追踪回到模拟世界里的光线。这个方法带来三个主要的优势: 它让我们容易得到现实世界的光学效应 (optical effect),如透明度 (transparency)、反射光 (reflected light)以及产生阴影 (cast shadows);它让我们可以直接用任何我们想要的几何的物体,来定义出模拟的世界,而不需要用多边形 (polygons)来建构它们;以及它很简单实现。
(defun sq (x) (* x x))
(defun mag (x y z)
(sqrt (+ (sq x) (sq y) (sq z))))
(defun unit-vector (x y z)
(let ((d (mag x y z)))
(values (/ x d) (/ y d) (/ z d))))
(defstruct (point (:conc-name nil))
x y z)
(defun distance (p1 p2)
(mag (- (x p1) (x p2))
(- (y p1) (y p2))
(- (z p1) (z p2))))
(defun minroot (a b c)
(if (zerop a)
(/ (- c) b)
(let ((disc (- (sq b) (* 4 a c))))
(unless (minusp disc)
(let ((discrt (sqrt disc)))
(min (/ (+ (- b) discrt) (* 2 a))
(/ (- (- b) discrt) (* 2 a))))))))
图 9.2 实用数学函数
图 9.2 包含了我们在光线追踪器里会需要用到的一些实用数学函数。第一个 sq ,返回其参数的平方。下一个 mag ,返回一个给定 x y z 所组成向量的大小 (magnitude)。这个函数被接下来两个函数用到。我们在 unit-vector 用到了,此函数返回三个数值,来表示与单位向量有着同样方向的向量,其中向量是由 x y z 所组成的:
> (multiple-value-call #'mag (unit-vector 23 12 47)) 1.0
我们在 distance 也用到了 mag ,它返回三维空间中,两点的距离。(定义 point 结构来有一个 nil 的 conc-name 意味着栏位存取的函数会有跟栏位一样的名字: 举例来说, x 而不是 point-x 。)
最后 minroot 接受三个实数, a , b 与 c ,并返回满足等式 \(ax^2+bx+c=0\) 的最小实数 x 。当 a 不为 \(0\) 时,这个等式的根由下面这个熟悉的式子给出:
图 9.3 包含了定义一个最小光线追踪器的代码。 它产生通过单一光源照射的黑白图像,与观测点 (eye)处于同个位置。 (结果看起来像是闪光摄影术 (flash photography)拍出来的)
surface 结构用来表示模拟世界中的物体。更精确的说,它会被 included 至定义具体类型物体的结构里,像是球体 (spheres)。 surface 结构本身只包含一个栏位: 一个 color 范围从 0 (黑色) 至 1 (白色)。
(defstruct surface color)
(defparameter *world* nil)
(defconstant eye (make-point :x 0 :y 0 :z 200))
(defun tracer (pathname &optional (res 1))
(with-open-file (p pathname :direction :output)
(format p "P2 ~A ~A 255" (* res 100) (* res 100))
(let ((inc (/ res)))
(do ((y -50 (+ y inc)))
((< (- 50 y) inc))
(do ((x -50 (+ x inc)))
((< (- 50 x) inc))
(print (color-at x y) p))))))
(defun color-at (x y)
(multiple-value-bind (xr yr zr)
(unit-vector (- x (x eye))
(- y (y eye))
(- 0 (z eye)))
(round (* (sendray eye xr yr zr) 255))))
(defun sendray (pt xr yr zr)
(multiple-value-bind (s int) (first-hit pt xr yr zr)
(if s
(* (lambert s int xr yr zr) (surface-color s))
0)))
(defun first-hit (pt xr yr zr)
(let (surface hit dist)
(dolist (s *world*)
(let ((h (intersect s pt xr yr zr)))
(when h
(let ((d (distance h pt)))
(when (or (null dist) (< d dist))
(setf surface s hit h dist d))))))
(values surface hit)))
(defun lambert (s int xr yr zr)
(multiple-value-bind (xn yn zn) (normal s int)
(max 0 (+ (* xr xn) (* yr yn) (* zr zn)))))
图 9.3 光线追踪。
图像平面会是由 x 轴与 y 轴所定义的平面。观测者 (eye) 会在 z 轴,距离原点 200 个单位。所以要在图像平面可以被看到,插入至 *worlds* 的表面 (一开始为 nil)会有着负的 z 座标。图 9.4 说明了一个光线穿过图像平面上的一点,并击中一个球体。
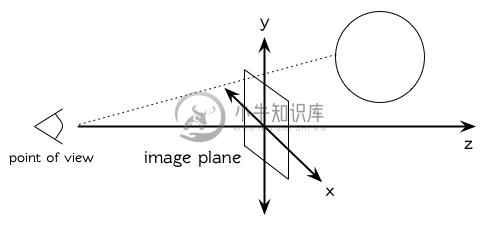
图 9.4: 追踪光线。
函数 tracer 接受一个路径名称,并写入一张图片至对应的文件。图片文件会用一种简单的 ASCII 称作 PGM 的格式写入。默认情况下,图像会是 100x100 。我们 PGM 文件的标头 (headers) 会由标签 P2 组成,伴随着指定图片宽度 (breadth)与高度 (height)的整数,初始为 100,单位为 pixel,以及可能的最大值 (255)。文件剩余的部份会由 10000 个介于 0 (黑)与 1 (白)整数组成,代表着 100 条 100 像素的水平线。
图片的解析度可以通过给入明确的 res 来调整。举例来说,如果 res 是 2 ,则同样的图像会被渲染成 200x200 。
图片是一个在图像平面 100x100 的正方形。每一个像素代表着穿过图像平面抵达观测点的光的数量。要找到每个像素光的数量, tracer 调用 color-at 。这个函数找到从观测点至该点的向量,并调用 sendray 来追踪这个向量回到模拟世界的轨迹; sandray 会返回一个数值介于 0 与 1 之间的亮度 (intensity),之后会缩放成一个 0 至 255 的整数来显示。
要决定一个光线的亮度, sendray 需要找到光是从哪个物体所反射的。要办到这件事,我们调用 first-hit ,此函数研究在 *world* 里的所有平面,并返回光线最先抵达的平面(如果有的话)。如果光没有击中任何东西, sendray 仅返回背景颜色,按惯例是 0 (黑色)。如果光线有击中某物的话,我们需要找出在光击中时,有多少数量的光照在该平面。
朗伯定律 告诉我们,由平面上一点所反射的光的强度,正比于该点的单位法向量 (unit normal vector) N (这里是与平面垂直且长度为一的向量)与该点至光源的单位向量 L 的点积 (dot-product):
\[i = N·L\]如果光刚好照到这点, N 与 L 会重合 (coincident),则点积会是最大值, 1 。如果将在这时候将平面朝光转 90 度,则 N 与 L 会垂直,则两者点积会是 0 。如果光在平面后面,则点积会是负数。
在我们的程序里,我们假设光源在观测点 (eye),所以 lambert 使用了这个规则来找到平面上某点的亮度 (illumination),返回我们追踪的光的单位向量与法向量的点积。
在 sendray 这个值会乘上平面的颜色 (即便是有好的照明,一个暗的平面还是暗的)来决定该点之后总体亮度。
为了简单起见,我们在模拟世界里会只有一种物体,球体。图 9.5 包含了与球体有关的代码。球体结构包含了 surface ,所以一个球体会有一种颜色以及 center 和 radius 。调用 defsphere 添加一个新球体至世界里。
(defstruct (sphere (:include surface))
radius center)
(defun defsphere (x y z r c)
(let ((s (make-sphere
:radius r
:center (make-point :x x :y y :z z)
:color c)))
(push s *world*)
s))
(defun intersect (s pt xr yr zr)
(funcall (typecase s (sphere #'sphere-intersect))
s pt xr yr zr))
(defun sphere-intersect (s pt xr yr zr)
(let* ((c (sphere-center s))
(n (minroot (+ (sq xr) (sq yr) (sq zr))
(* 2 (+ (* (- (x pt) (x c)) xr)
(* (- (y pt) (y c)) yr)
(* (- (z pt) (z c)) zr)))
(+ (sq (- (x pt) (x c)))
(sq (- (y pt) (y c)))
(sq (- (z pt) (z c)))
(- (sq (sphere-radius s)))))))
(if n
(make-point :x (+ (x pt) (* n xr))
:y (+ (y pt) (* n yr))
:z (+ (z pt) (* n zr))))))
(defun normal (s pt)
(funcall (typecase s (sphere #'sphere-normal))
s pt))
(defun sphere-normal (s pt)
(let ((c (sphere-center s)))
(unit-vector (- (x c) (x pt))
(- (y c) (y pt))
(- (z c) (z pt)))))
图 9.5 球体。
函数 intersect 判断与何种平面有关,并调用对应的函数。在此时只有一种, sphere-intersect ,但 intersect 是写成可以容易扩展处理别种物体。
我们要怎么找到一束光与一个球体的交点 (intersection)呢?光线是表示成点 \(p =〈x_0,y_0,x_0〉\) 以及单位向量 \(v =〈x_r,y_r,x_r〉\) 。每个在光上的点可以表示为 \(p+nv\) ,对于某个 n ── 即 \(〈x_0+nx_r,y_0+ny_r,z_0+nz_r〉\) 。光击中球体的点的距离至中心 \(〈x_c,y_c,z_c〉\) 会等于球体的半径 r 。所以在下列这个交点的方程序会成立:
\[r = \sqrt{ (x_0 + nx_r - x_c)^2 + (y_0 + ny_r - y_c)^2 + (z_0 + nz_r - z_c)^2 }\]这会给出
\[an^2 + bn + c = 0\]其中
\[\begin{split}a = x_r^2 + y_r^2 + z_r^2\\b = 2((x_0-x_c)x_r + (y_0-y_c)y_r + (z_0-z_c)z_r)\\c = (x_0-x_c)^2 + (y_0-y_c)^2 + (z_0-z_c)^2 - r^2\end{split}\]要找到交点我们只需要找到这个二次方程序的根。它可能是零、一个或两个实数根。没有根代表光没有击中球体;一个根代表光与球体交于一点 (擦过 「grazing hit」);两个根代表光与球体交于两点 (一点交于进入时、一点交于离开时)。在最后一个情况里,我们想要两个根之中较小的那个; n 与光离开观测点的距离成正比,所以先击中的会是较小的 n 。所以我们调用 minroot 。如果有一个根, sphere-intersect 返回代表该点的 \(〈x_0+nx_r,y_0+ny_r,z_0+nz_r〉\) 。
图 9.5 的另外两个函数, normal 与 sphere-normal 类比于 intersect 与 sphere-intersect 。要找到垂直于球体很简单 ── 不过是从该点至球体中心的向量而已。
图 9.6 示范了我们如何产生图片; ray-test 定义了 38 个球体(不全都看的见)然后产生一张图片,叫做 “sphere.pgm” 。
(译注:PGM 可移植灰度图格式,更多信息参见 wiki )
(defun ray-test (&optional (res 1))
(setf *world* nil)
(defsphere 0 -300 -1200 200 .8)
(defsphere -80 -150 -1200 200 .7)
(defsphere 70 -100 -1200 200 .9)
(do ((x -2 (1+ x)))
((> x 2))
(do ((z 2 (1+ z)))
((> z 7))
(defsphere (* x 200) 300 (* z -400) 40 .75)))
(tracer (make-pathname :name "spheres.pgm") res))
图 9.6 使用光线追踪器
图 9.7 是产生出来的图片,其中 res 参数为 10。

图 9.7: 追踪光线的图
一个实际的光线追踪器可以产生更复杂的图片,因为它会考虑更多,我们只考虑了单一光源至平面某一点。可能会有多个光源,每一个有不同的强度。它们通常不会在观测点,在这个情况程序需要检查至光源的向量是否与其他平面相交,这会在第一个相交的平面上产生阴影。将光源放置于观测点让我们不需要考虑这麽复杂的情况,因为我们看不见在阴影中的任何点。
一个实际的光线追踪器不仅追踪光第一个击中的平面,也会加入其它平面的反射光。一个实际的光线追踪器会是有颜色的,并可以模型化出透明或是闪耀的平面。但基本的算法会与图 9.3 所演示的差不多,而许多改进只需要递回的使用同样的成分。
一个实际的光线追踪器可以是高度优化的。这里给出的程序为了精简写成,甚至没有如 Lisp 程序员会最佳化的那样,就仅是一个光线追踪器而已。仅加入类型与行内宣告 (13.3 节)就可以让它变得两倍以上快。
Chapter 9 总结 (Summary)
- Common Lisp 提供整数 (integers)、比值 (ratios)、浮点数 (floating-point numbers)以及复数 (complex numbers)。
- 数字可以被约分或转换 (converted),而它们的位数 (components)可以被取出。
- 用来比较数字的谓词可以接受任意数量的参数,以及比较下一数对 (successive pairs) ── /= 函数除外,它是用来比较所有的数对 (pairs)。
- Common Lisp 几乎提供你在低阶科学计算机可以看到的数值函数。同样的函数普遍可应用在多种类型的数字上。
- Fixnum 是小至可以塞入一个字 (word)的整数。它们在必要时会悄悄但花费昂贵地转成大数 (bignum)。Common Lisp 提供最多四种浮点数。每一个浮点表示法的限制是实现相关的 (implementation-dependent)常量。
- 一个光线追踪器 (ray-tracer)通过追踪光线来产生图像,使得每一像素回到模拟的世界。
Chapter 9 练习 (Exercises)
- 定义一个函数,接受一个实数列表,若且唯若 (iff)它们是非递减 (nondecreasing)顺序时返回真。
- 定义一个函数,接受一个整数
cents并返回四个值,将数字用25-,10-,5-,1-来显示,使用最少数量的硬币。(译注:25-是 25 美分,以此类推) - 一个遥远的星球住着两种生物, wigglies 与 wobblies 。 Wigglies 与 wobblies 唱歌一样厉害。每年都有一个比赛来选出十大最佳歌手。下面是过去十年的结果:
| YEAR | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| WIGGLIES | 6 | 5 | 6 | 4 | 5 | 5 | 4 | 5 | 6 | 5 |
| WOBBLIES | 4 | 5 | 4 | 6 | 5 | 5 | 6 | 5 | 4 | 5 |
写一个程序来模拟这样的比赛。你的结果实际上有建议委员会每年选出 10 个最佳歌手吗?
- 定义一个函数,接受 8 个表示二维空间中两个线段端点的实数,若线段没有相交,则返回假,或返回两个值表示相交点的
x座标与y座标。 - 假设
f是一个接受一个 (实数) 参数的函数,而min与max是有着不同正负号的非零实数,使得f对于参数i有一个根 (返回零)并满足min < i < max。定义一个函数,接受四个参数,f,min,max以及epsilon,并返回一个i的近似值,准确至正负epsilon之内。 - Honer’s method 是一个有效率求出多项式的技巧。要找到 \(ax^3+bx^2+cx+d\) 你对
x(x(ax+b)+c)+d求值。定义一个函数,接受一个或多个参数 ── x 的值伴随着 n 个实数,用来表示(n-1)次方的多项式的系数 ── 并用 Honer’s method 计算出多项式的值。
- 你的 Common Lisp 实现使用了几个位元来表示定长数?
- 你的 Common Lisp 实现提供几种不同的浮点数?
脚注
| [1] | 当 format 取整显示时,它不保证会取成偶数或奇数。见 125 页 (译注: 7.4 节)。 |

