第四章:特殊数据结构
在之前的章节里,我们讨论了列表,Lisp 最多功能的数据结构。本章将演示如何使用 Lisp 其它的数据结构:数组(包含向量与字符串),结构以及哈希表。它们或许不像列表这么灵活,但存取速度更快并使用了更少空间。
Common Lisp 还有另一种数据结构:实例(instance)。实例将在 11 章讨论,讲述 CLOS。
4.1 数组 (Array)
在 Common Lisp 里,你可以调用 make-array 来构造一个数组,第一个实参为一个指定数组维度的列表。要构造一个 2 x 3 的数组,我们可以:
> (setf arr (make-array '(2 3) :initial-element nil)) #<Simple-Array T (2 3) BFC4FE>
Common Lisp 的数组至少可以达到七个维度,每个维度至少可以容纳 1023 个元素。
:initial-element 实参是选择性的。如果有提供这个实参,整个数组会用这个值作为初始值。若试着取出未初始化的数组内的元素,其结果为未定义(undefined)。
用 aref 取出数组内的元素。与 Common Lisp 的存取函数一样, aref 是零索引的(zero-indexed):
> (aref arr 0 0) NIL
要替换数组的某个元素,我们使用 setf 与 aref :
> (setf (aref arr 0 0) 'b) B > (aref arr 0 0) B
要表示字面常量的数组(literal array),使用 #na 语法,其中 n 是数组的维度。举例来说,我们可以这样表示 arr 这个数组:
#2a((b nil nil) (nil nil nil))
如果全局变量 *print-array* 为真,则数组会用以下形式来显示:
> (setf *print-array* t) T > arr #2A((B NIL NIL) (NIL NIL NIL))
如果我们只想要一维的数组,你可以给 make-array 第一个实参传一个整数,而不是一个列表:
> (setf vec (make-array 4 :initial-element nil)) #(NIL NIL NIL NIL)
一维数组又称为向量(vector)。你可以通过调用 vector 来一步骤构造及填满向量,向量的元素可以是任何类型:
> (vector "a" 'b 3)
#("a" b 3)
字面常量的数组可以表示成 #na ,字面常量的向量也可以用这种语法表达。
可以用 aref 来存取向量,但有一个更快的函数叫做 svref ,专门用来存取向量。
> (svref vec 0) NIL
在 svref 内的 “sv” 代表“简单向量”(“simple vector”),所有的向量缺省是简单向量。 [1]
4.2 示例:二叉搜索 (Example: Binary Search)
作为一个示例,这小节演示如何写一个在排序好的向量里搜索对象的函数。如果我们知道一个向量是排序好的,我们可以比(65页) find 做的更好, find 必须依序检查每一个元素。我们可以直接跳到向量中间开始找。如果中间的元素是我们要找的对象,搜索完毕。要不然我们持续往左半部或往右半部搜索,取决于对象是小于或大于中间的元素。
图 4.1 包含了一个这么工作的函数。其实这两个函数: bin-search 设置初始范围及发送控制信号给 finder , finder 寻找向量 vec 内 obj 是否介于 start 及 end 之间。
(defun bin-search (obj vec)
(let ((len (length vec)))
(and (not (zerop len))
(finder obj vec 0 (- len 1)))))
(defun finder (obj vec start end)
(let ((range (- end start)))
(if (zerop range)
(if (eql obj (aref vec start))
obj
nil)
(let ((mid (+ start (round (/ range 2)))))
(let ((obj2 (aref vec mid)))
(if (< obj obj2)
(finder obj vec start (- mid 1))
(if (> obj obj2)
(finder obj vec (+ mid 1) end)
obj)))))))
图 4.1: 搜索一个排序好的向量
如果要找的 range 缩小至一个元素,而如果这个元素是 obj 的话,则 finder 直接返回这个元素,反之返回 nil 。如果 range 大于 1 ,我们設置 middle ( round 返回离实参最近的整数) 為 obj2 。如果 obj 小于 obj2 ,则递归地往向量的左半部寻找。如果 obj 大于 obj2 ,则递归地往向量的右半部寻找。剩下的一个选择是 obj=obj2 ,在这个情况我们找到要找的元素,直接返回这个元素。
如果我们插入下面这行至 finder 的起始处:
(format t "~A~%" (subseq vec start (+ end 1)))
我们可以观察被搜索的元素的数量,是每一步往左减半的:
> (bin-search 3 #(0 1 2 3 4 5 6 7 8 9)) #(0 1 2 3 4 5 6 7 8 9) #(0 1 2 3) #(3) 3
4.3 字符与字符串 (Strings and Characters)
字符串是字符组成的向量。我们用一系列由双引号包住的字符,来表示一个字符串常量,而字符 c 用 #\c 表示。
每个字符都有一个相关的整数 ── 通常是 ASCII 码,但不一定是。在多数的 Lisp 实现里,函数 char-code 返回与字符相关的数字,而 code-char 返回与数字相关的字符。
字符比较函数 char< (小于), char<= (小于等于), char= (等于), char>= (大于等于) , char> (大于),以及 char/= (不同)。他们的工作方式和 146 页(译注 9.3 节)比较数字用的操作符一样。
> (sort "elbow" #'char<) "below"
由于字符串是字符向量,序列与数组的函数都可以用在字符串。你可以用 aref 来取出元素,举例来说,
> (aref "abc" 1) #\b
但针对字符串可以使用更快的 char 函数:
> (char "abc" 1) #\b
可以使用 setf 搭配 char (或 aref )来替换字符串的元素:
> (let ((str (copy-seq "Merlin"))) (setf (char str 3) #\k) str)
如果你想要比较两个字符串,你可以使用通用的 equal 函数,但还有一个比较函数,是忽略字母大小写的 string-equal :
> (equal "fred" "fred") T > (equal "fred" "Fred") NIL >(string-equal "fred" "Fred") T
Common Lisp 提供大量的操控、比较字符串的函数。收录在附录 D,从 364 页开始。
有许多方式可以创建字符串。最普遍的方式是使用 format 。将第一个参数设为 nil 来调用 format ,使它返回一个原本会印出来的字符串:
> (format nil "~A or ~A" "truth" "dare") "truth or dare"
但若你只想把数个字符串连结起来,你可以使用 concatenate ,它接受一个特定类型的符号,加上一个或多个序列:
> (concatenate 'string "not " "to worry") "not to worry"
4.4 序列 (Sequences)
在 Common Lisp 里,序列类型包含了列表与向量(因此也包含了字符串)。有些用在列表的函数,实际上是序列函数,包括 remove 、 length 、 subseq 、 reverse 、 sort 、 every 以及 some 。所以 46 页(译注 3.11 小节的 mirror? 函数)我们所写的函数,也可以用在其他种类的序列上:
> (mirror? "abba") T
我们已经看过四种用来取出序列元素的函数: 给列表使用的 nth , 给向量使用的 aref 及 svref ,以及给字符串使用的 char 。 Common Lisp 也提供了通用的 elt ,对任何种类的序列都有效:
> (elt '(a b c) 1) B
针对特定类型的序列,特定的存取函数会比较快,所以使用 elt 是没有意义的,除非在代码当中,有需要支持通用序列的地方。
使用 elt ,我们可以写一个针对向量来说更有效率的 mirror? 版本:
(defun mirror? (s)
(let ((len (length s)))
(and (evenp len)
(do ((forward 0 (+ forward 1))
(back (- len 1) (- back 1)))
((or (> forward back)
(not (eql (elt s forward)
(elt s back))))
(> forward back))))))
这个版本也可用在列表,但这个实现更适合给向量使用。频繁的对列表调用 elt 的代价是昂贵的,因为列表仅允许顺序存取。而向量允许随机存取,从任何元素来存取每一个元素都是廉价的。
许多序列函数接受一个或多个,由下表所列的标准关键字参数:
| 参数 | 用途 | 缺省值 |
|---|---|---|
| :key | 应用至每个元素的函数 | identity |
| :test | 作来比较的函数 | eql |
| :from-end | 若为真,反向工作。 | nil |
| :start | 起始位置 | 0 |
| :end | 若有给定,结束位置。 | nil |
一个接受所有关键字参数的函数是 position ,返回序列中一个元素的位置,未找到元素时则返回 nil 。我们使用 position 来演示关键字参数所扮演的角色。
> (position #\a "fantasia") 1 > (position #\a "fantasia" :start 3 :end 5) 4
第二个例子我们要找在第四个与第六个字符间,第一个 a 所出现的位置。 :start 关键字参数是第一个被考虑的元素位置,缺省是序列的第一个元素。 :end 关键字参数,如果有给的话,是第一个不被考虑的元素位置。
如果我们给入 :from-end 关键字参数,
> (position #\a "fantasia" :from-end t) 7
我们得到最靠近结尾的 a 的位置。但位置是像平常那样计算;而不是从尾端算回来的距离。
:key 关键字参数是序列中每个元素在被考虑之前,应用至元素上的函数。如果我们说,
> (position 'a '((c d) (a b)) :key #'car) 1
那么我们要找的是,元素的 car 部分是符号 a 的第一个元素。
:test 关键字参数接受需要两个实参的函数,并定义了怎样是一个成功的匹配。缺省函数为 eql 。如果你想要匹配一个列表,你也许想使用 equal 来取代:
> (position '(a b) '((a b) (c d))) NIL > (position '(a b) '((a b) (c d)) :test #'equal) 0
:test 关键字参数可以是任何接受两个实参的函数。举例来说,给定 < ,我们可以询问第一个使第一个参数比它小的元素位置:
> (position 3 '(1 0 7 5) :test #'<) 2
使用 subseq 与 position ,我们可以写出分开序列的函数。举例来说,这个函数
(defun second-word (str)
(let ((p1 (+ (position #\ str) 1)))
(subseq str p1 (position #\ str :start p1))))
返回字符串中第一个单字空格后的第二个单字:
> (second-word "Form follows function") "follows"
要找到满足谓词的元素,其中谓词接受一个实参,我们使用 position-if 。它接受一个函数与序列,并返回第一个满足此函数的元素:
> (position-if #'oddp '(2 3 4 5)) 1
position-if 接受除了 :test 之外的所有关键字参数。
有许多相似的函数,如给序列使用的 member 与 member-if 。分别是, find (接受全部关键字参数)与 find-if (接受除了 :test 之外的所有关键字参数):
> (find #\a "cat") #\a > (find-if #'characterp "ham") #\h
不同于 member 与 member-if ,它们仅返回要寻找的对象。
通常一个 find-if 的调用,如果解读为 find 搭配一个 :key 关键字参数的话,会显得更清楚。举例来说,表达式
(find-if #'(lambda (x)
(eql (car x) 'complete))
lst)
可以更好的解读为
(find 'complete lst :key #'car)
函数 remove (22 页)以及 remove-if 通常都可以用在序列。它们跟 find 与 find-if 是一样的关系。另一个相关的函数是 remove-duplicates ,仅保留序列中每个元素的最后一次出现。
> (remove-duplicates "abracadabra") "cdbra"
这个函数接受前表所列的所有关键字参数。
函数 reduce 用来把序列压缩成一个值。它至少接受两个参数,一个函数与序列。函数必须是接受两个实参的函数。在最简单的情况下,一开始函数用序列前两个元素作为实参来调用,之后接续的元素作为下次调用的第二个实参,而上次返回的值作为下次调用的第一个实参。最后调用最终返回的值作为 reduce 整个函数的返回值。也就是说像是这样的表达式:
(reduce #'fn '(a b c d))
等同于
(fn (fn (fn 'a 'b) 'c) 'd)
我们可以使用 reduce 来扩充只接受两个参数的函数。举例来说,要得到三个或多个列表的交集(intersection),我们可以:
> (reduce #'intersection '((b r a d 's) (b a d) (c a t))) (A)
4.5 示例:解析日期 (Example: Parsing Dates)
作为序列操作的示例,本节演示了如何写程序来解析日期。我们将编写一个程序,可以接受像是 “16 Aug 1980” 的字符串,然后返回一个表示日、月、年的整数列表。
(defun tokens (str test start)
(let ((p1 (position-if test str :start start)))
(if p1
(let ((p2 (position-if #'(lambda (c)
(not (funcall test c)))
str :start p1)))
(cons (subseq str p1 p2)
(if p2
(tokens str test p2)
nil)))
nil)))
(defun constituent (c)
(and (graphic-char-p c)
(not (char= c #\ ))))
图 4.2 辨别符号 (token)
图 4.2 里包含了某些在这个应用里所需的通用解析函数。第一个函数 tokens ,用来从字符串中取出语元 (token)。给定一个字符串及测试函数,满足测试函数的字符组成子字符串,子字符串再组成列表返回。举例来说,如果测试函数是对字母返回真的 alpha-char-p 函数,我们得到:
> (tokens "ab12 3cde.f" #'alpha-char-p 0)
("ab" "cde" "f")
所有不满足此函数的字符被视为空白 ── 他们是语元的分隔符,但永远不是语元的一部分。
函数 constituent 被定义成用来作为 tokens 的实参。
在 Common Lisp 里,图形字符是我们可见的字符,加上空白字符。所以如果我们用 constituent 作为测试函数时,
> (tokens "ab12 3cde.f gh" #'constituent 0)
("ab12" "3cde.f" "gh")
则语元将会由空白区分出来。
图 4.3 包含了特别为解析日期打造的函数。函数 parse-date 接受一个特别形式组成的日期,并返回代表这个日期的整数列表:
> (parse-date "16 Aug 1980") (16 8 1980)
(defun parse-date (str)
(let ((toks (tokens str #'constituent 0)))
(list (parse-integer (first toks))
(parse-month (second toks))
(parse-integer (third toks)))))
(defconstant month-names
#("jan" "feb" "mar" "apr" "may" "jun"
"jul" "aug" "sep" "oct" "nov" "dec"))
(defun parse-month (str)
(let ((p (position str month-names
:test #'string-equal)))
(if p
(+ p 1)
nil)))
图 4.3 解析日期的函数
parse-date 使用 tokens 来解析日期字符串,接着调用 parse-month 及 parse-integer 来转译年、月、日。要找到月份,调用 parse-month ,由于使用的是 string-equal 来匹配月份的名字,所以输入可以不分大小写。要找到年和日,调用内置的 parse-integer , parse-integer 接受一个字符串并返回对应的整数。
如果需要自己写程序来解析整数,也许可以这么写:
(defun read-integer (str)
(if (every #'digit-char-p str)
(let ((accum 0))
(dotimes (pos (length str))
(setf accum (+ (* accum 10)
(digit-char-p (char str pos)))))
accum)
nil))
这个定义演示了在 Common Lisp 中,字符是如何转成数字的 ── 函数 digit-char-p 不仅测试字符是否为数字,同时返回了对应的整数。
4.6 结构 (Structures)
结构可以想成是豪华版的向量。假设你要写一个程序来追踪长方体。你可能会想用三个向量元素来表示长方体:高度、宽度及深度。与其使用原本的 svref ,不如定义像是下面这样的抽象,程序会变得更容易阅读,
(defun block-height (b) (svref b 0))
而结构可以想成是,这些函数通通都替你定义好了的向量。
要想定义结构,使用 defstruct 。在最简单的情况下,只要给出结构及字段的名字便可以了:
(defstruct point x y)
这里定义了一个 point 结构,具有两个字段 x 与 y 。同时隐式地定义了 make-point 、 point-p 、 copy-point 、 point-x 及 point-y 函数。
2.3 节提过, Lisp 程序可以写出 Lisp 程序。这是目前所见的明显例子之一。当你调用 defstruct 时,它自动生成了其它几个函数的定义。有了宏以后,你将可以自己来办到同样的事情(如果需要的话,你甚至可以自己写出 defstruct )。
每一个 make-point 的调用,会返回一个新的 point 。可以通过给予对应的关键字参数,来指定单一字段的值:
(setf p (make-point :x 0 :y 0)) #S(POINT X 0 Y 0)
存取 point 字段的函数不仅被定义成可取出数值,也可以搭配 setf 一起使用。
> (point-x p) 0 > (setf (point-y p) 2) 2 > p #S(POINT X 0 Y 2)
定义结构也定义了以结构为名的类型。每个点的类型层级会是,类型 point ,接着是类型 structure ,再来是类型 atom ,最后是 t 类型。所以使用 point-p 来测试某个东西是不是一个点时,也可以使用通用性的函数,像是 typep 来测试。
> (point-p p) T > (typep p 'point) T
我们可以在本来的定义中,附上一个列表,含有字段名及缺省表达式,来指定结构字段的缺省值。
(defstruct polemic
(type (progn
(format t "What kind of polemic was it? ")
(read)))
(effect nil))
如果 make-polemic 调用没有给字段指定初始值,则字段会被设成缺省表达式的值:
> (make-polemic) What kind of polemic was it? scathing #S(POLEMIC :TYPE SCATHING :EFFECT NIL)
结构显示的方式也可以控制,以及结构自动产生的存取函数的字首。以下是做了前述两件事的 point 定义:
(defstruct (point (:conc-name p)
(:print-function print-point))
(x 0)
(y 0))
(defun print-point (p stream depth)
(format stream "#<~A, ~A>" (px p) (py p)))
:conc-name 关键字参数指定了要放在字段前面的名字,并用这个名字来生成存取函数。预设是 point- ;现在变成只有 p 。不使用缺省的方式使代码的可读性些微降低了,只有在需要常常用到这些存取函数时,你才会想取个短点的名字。
:print-function 是在需要显示结构出来看时,指定用来打印结构的函数 ── 需要显示的情况比如,要在顶层显示时。这个函数需要接受三个实参:要被印出的结构,在哪里被印出,第三个参数通常可以忽略。 [2] 我们会在 7.1 节讨论流(stream)。现在来说,只要知道流可以作为参数传给 format 就好了。
函数 print-point 会用缩写的形式来显示点:
> (make-point) #<0,0>
4.7 示例:二叉搜索树 (Example: Binary Search Tree)
由于 sort 本身系统就有了,极少需要在 Common Lisp 里编写排序程序。本节将演示如何解决一个与此相关的问题,这个问题尚未有现成的解决方案:维护一个已排序的对象集合。本节的代码会把对象存在二叉搜索树里( binary search tree )或称作 BST。当二叉搜索树平衡时,允许我们可以在与时间成 log n 比例的时间内,来寻找、添加或是删除元素,其中 n 是集合的大小。
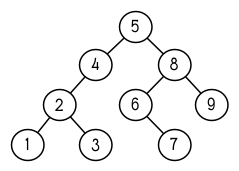
图 4.4: 二叉搜索树
二叉搜索树是一种二叉树,给定某个排序函数,比如 < ,每个元素的左子树都 < 该元素,而该元素 < 其右子树。图 4.4 展示了根据 < 排序的二叉树。
图 4.5 包含了二叉搜索树的插入与寻找的函数。基本的数据结构会是 node (节点),节点有三个部分:一个字段表示存在该节点的对象,以及各一个字段表示节点的左子树及右子树。可以把节点想成是有一个 car 和两个 cdr 的一个 cons 核(cons cell)。
(defstruct (node (:print-function
(lambda (n s d)
(format s "#<~A>" (node-elt n)))))
elt (l nil) (r nil))
(defun bst-insert (obj bst <)
(if (null bst)
(make-node :elt obj)
(let ((elt (node-elt bst)))
(if (eql obj elt)
bst
(if (funcall < obj elt)
(make-node
:elt elt
:l (bst-insert obj (node-l bst) <)
:r (node-r bst))
(make-node
:elt elt
:r (bst-insert obj (node-r bst) <)
:l (node-l bst)))))))
(defun bst-find (obj bst <)
(if (null bst)
nil
(let ((elt (node-elt bst)))
(if (eql obj elt)
bst
(if (funcall < obj elt)
(bst-find obj (node-l bst) <)
(bst-find obj (node-r bst) <))))))
(defun bst-min (bst)
(and bst
(or (bst-min (node-l bst)) bst)))
(defun bst-max (bst)
(and bst
(or (bst-max (node-r bst)) bst)))
图 4.5 二叉搜索树:查询与插入
一棵二叉搜索树可以是 nil 或是一个左子、右子树都是二叉搜索树的节点。如同列表可由连续调用 cons 来构造,二叉搜索树将可以通过连续调用 bst-insert 来构造。这个函数接受一个对象,一棵二叉搜索树及一个排序函数,并返回将对象插入的二叉搜索树。和 cons 函数一样, bst-insert 不改动做为第二个实参所传入的二叉搜索树。以下是如何使用这个函数来构造一棵叉搜索树:
> (setf nums nil)
NIL
> (dolist (x '(5 8 4 2 1 9 6 7 3))
(setf nums (bst-insert x nums #'<)))
NIL
图 4.4 显示了此时 nums 的结构所对应的树。
我们可以使用 bst-find 来找到二叉搜索树中的对象,它与 bst-insert 接受同样的参数。先前叙述所提到的 node 结构,它像是一个具有两个 cdr 的 cons 核。如果我们把 16 页的 our-member 拿来与 bst-find 比较的话,这样的类比更加明确。
与 member 相同, bst-find 不仅返回要寻找的元素,也返回了用寻找元素做为根节点的子树:
> (bst-find 12 nums #'<) NIL > (bst-find 4 nums #'<) #<4>
这使我们可以区分出无法找到某个值,以及成功找到 nil 的情况。
要找到二叉搜索树的最小及最大的元素是很简单的。要找到最小的,我们沿着左子树的路径走,如同 bst-min 所做的。要找到最大的,沿着右子树的路径走,如同 bst-max 所做的:
> (bst-min nums) #<1> > (bst-max nums) #<9>
要从二叉搜索树里移除元素一样很快,但需要更多代码。图 4.6 演示了如何从二叉搜索树里移除元素。
(defun bst-remove (obj bst <)
(if (null bst)
nil
(let ((elt (node-elt bst)))
(if (eql obj elt)
(percolate bst)
(if (funcall < obj elt)
(make-node
:elt elt
:l (bst-remove obj (node-l bst) <)
:r (node-r bst))
(make-node
:elt elt
:r (bst-remove obj (node-r bst) <)
:l (node-l bst)))))))
(defun percolate (bst)
(cond ((null (node-l bst))
(if (null (node-r bst))
nil
(rperc bst)))
((null (node-r bst)) (lperc bst))
(t (if (zerop (random 2))
(lperc bst)
(rperc bst)))))
(defun rperc (bst)
(make-node :elt (node-elt (node-r bst))
:l (node-l bst)
:r (percolate (node-r bst))))
图 4.6 二叉搜索树:移除
勘误: 此版 bst-remove 的定义已被汇报是坏掉的,请参考 这里 获得修复版。
函数 bst-remove 接受一个对象,一棵二叉搜索树以及排序函数,并返回一棵与本来的二叉搜索树相同的树,但不包含那个要移除的对象。和 remove 一样,它不改动做为第二个实参所传入的二叉搜索树:
> (setf nums (bst-remove 2 nums #'<)) #<5> > (bst-find 2 nums #'<) NIL
此时 nums 的结构应该如图 4.7 所示。 (另一个可能性是 1 取代了 2 的位置。)
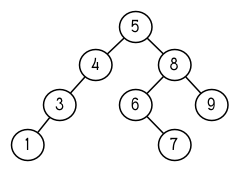
图 4.7: 二叉搜索树
移除需要做更多工作,因为从内部节点移除一个对象时,会留下一个空缺,需要由其中一个孩子来填补。这是 percolate 函数的用途。当它替换一个二叉搜索树的树根(topmost element)时,会找其中一个孩子来替换,并用此孩子的孩子来填补,如此这般一直递归下去。
为了要保持树的平衡,如果有两个孩子时, perlocate 随机择一替换。表达式 (random 2) 会返回 0 或 1 ,所以 (zerop (random 2)) 会返回真或假。
(defun bst-traverse (fn bst)
(when bst
(bst-traverse fn (node-l bst))
(funcall fn (node-elt bst))
(bst-traverse fn (node-r bst))))
图 4.8 二叉搜索树:遍历
一旦我们把一个对象集合插入至二叉搜索树时,中序遍历会将它们由小至大排序。这是图 4.8 中, bst-traverse 函数的用途:
> (bst-traverse #'princ nums) 13456789 NIL
(函数 princ 仅显示单一对象)
本节所给出的代码,提供了一个二叉搜索树实现的脚手架。你可能想根据应用需求,来充实这个脚手架。举例来说,这里所给出的代码每个节点只有一个 elt 字段;在许多应用里,有两个字段会更有意义, key 与 value 。本章的这个版本把二叉搜索树视为集合看待,从这个角度看,重复的插入是被忽略的。但是代码可以很简单地改动,来处理重复的元素。
二叉搜索树不仅是维护一个已排序对象的集合的方法。他们是否是最好的方法,取决于你的应用。一般来说,二叉搜索树最适合用在插入与删除是均匀分布的情况。有一件二叉搜索树不擅长的事,就是用来维护优先队列(priority queues)。在一个优先队列里,插入也许是均匀分布的,但移除总是在一个另一端。这会导致一个二叉搜索树变得不平衡,而我们期望的复杂度是 O(log(n)) 插入与移除操作,将会变成 O(n) 。如果用二叉搜索树来表示一个优先队列,也可以使用一般的列表,因为二叉搜索树最终会作用的像是个列表。
4.8 哈希表 (Hash Table)
第三章演示过列表可以用来表示集合(sets)与映射(mappings)。但当列表的长度大幅上升时(或是 10 个元素),使用哈希表的速度比较快。你通过调用 make-hash-table 来构造一个哈希表,它不需要传入参数:
> (setf ht (make-hash-table)) #<Hash-Table BF0A96>
和函数一样,哈希表总是用 #<...> 的形式来显示。
一个哈希表,与一个关联列表类似,是一种表达对应关系的方式。要取出与给定键值有关的数值,我们调用 gethash 并传入一个键值与哈希表。预设情况下,如果没有与这个键值相关的数值, gethash 会返回 nil 。
> (gethash 'color ht) NIL NIL
在这里我们首次看到 Common Lisp 最突出的特色之一:一个表达式竟然可以返回多个数值。函数 gethash 返回两个数值。第一个值是与键值有关的数值,第二个值说明了哈希表是否含有任何用此键值来储存的数值。由于第二个值是 nil ,我们知道第一个 nil 是缺省的返回值,而不是因为 nil 是与 color 有关的数值。
大部分的实现会在顶层显示一个函数调用的所有返回值,但仅期待一个返回值的代码,只会收到第一个返回值。 5.5 节会说明,代码如何接收多个返回值。
要把数值与键值作关联,使用 gethash 搭配 setf :
> (setf (gethash 'color ht) 'red) RED
现在如果我们再次调用 gethash ,我们会得到我们刚插入的值:
> (gethash 'color ht) RED T
第二个返回值证明,我们取得了一个真正储存的对象,而不是预设值。
存在哈希表的对象或键值可以是任何类型。举例来说,如果我们要保留函数的某种讯息,我们可以使用哈希表,用函数作为键值,字符串作为词条(entry):
> (setf bugs (make-hash-table))
#<Hash-Table BF4C36>
> (push "Doesn't take keyword arguments."
(gethash #'our-member bugs))
("Doesn't take keyword arguments.")
由于 gethash 缺省返回 nil ,而 push 是 setf 的缩写,可以轻松的给哈希表新添一个词条。 (有困扰的 our-member 定义在 16 页。)
可以用哈希表来取代用列表表示集合。当集合变大时,哈希表的查询与移除会来得比较快。要新增一个成员到用哈希表所表示的集合,把 gethash 用 setf 设成 t :
> (setf fruit (make-hash-table)) #<Hash-Table BFDE76> > (setf (gethash 'apricot fruit) t) T
然后要测试是否为成员,你只要调用:
> (gethash 'apricot fruit) T T
由于 gethash 缺省返回真,一个新创的哈希表,会很方便地是一个空集合。
要从集合中移除一个对象,你可以调用 remhash ,它从一个哈希表中移除一个词条:
> (remhash 'apricot fruit) T
返回值说明了是否有词条被移除;在这个情况里,有。
哈希表有一个迭代函数: maphash ,它接受两个实参,接受两个参数的函数以及哈希表。该函数会被每个键值对调用,没有特定的顺序:
> (setf (gethash 'shape ht) 'spherical
(gethash 'size ht) 'giant)
GIANT
> (maphash #'(lambda (k v)
(format t "~A = ~A~%" k v))
ht)
SHAPE = SPHERICAL
SIZE = GIANT
COLOR = RED
NIL
maphash 总是返回 nil ,但你可以通过传入一个会累积数值的函数,把哈希表的词条存在列表里。
哈希表可以容纳任何数量的元素,但当哈希表空间用完时,它们会被扩张。如果你想要确保一个哈希表,从特定数量的元素空间大小开始时,可以给 make-hash-table 一个选择性的 :size 关键字参数。做这件事情有两个理由:因为你知道哈希表会变得很大,你想要避免扩张它;或是因为你知道哈希表会是很小,你不想要浪费内存。 :size 参数不仅指定了哈希表的空间,也指定了元素的数量。平均来说,在被扩张前所能够容纳的数量。所以
(make-hash-table :size 5)
会返回一个预期存放五个元素的哈希表。
和任何牵涉到查询的结构一样,哈希表一定有某种比较键值的概念。预设是使用 eql ,但你可以提供一个额外的关键字参数 :test 来告诉哈希表要使用 eq , equal ,还是 equalp :
> (setf writers (make-hash-table :test #'equal)) #<Hash-Table C005E6> > (setf (gethash '(ralph waldo emerson) writers) t) T
这是一个让哈希表变得有效率的取舍之一。有了列表,我们可以指定 member 为判断相等性的谓词。有了哈希表,我们可以预先决定,并在哈希表构造时指定它。
大多数 Lisp 编程的取舍(或是生活,就此而论)都有这种特质。起初你想要事情进行得流畅,甚至赔上效率的代价。之后当代码变得沉重时,你牺牲了弹性来换取速度。
Chapter 4 总结 (Summary)
- Common Lisp 支持至少 7 个维度的数组。一维数组称为向量。
- 字符串是字符的向量。字符本身就是对象。
- 序列包括了向量与列表。许多序列函数都接受标准的关键字参数。
- 处理字符串的函数非常多,所以用 Lisp 来解析字符串是小菜一碟。
- 调用
defstruct定义了一个带有命名字段的结构。它是一个程序能写出程序的好例子。 - 二叉搜索树见长于维护一个已排序的对象集合。
- 哈希表提供了一个更有效率的方式来表示集合与映射 (mappings)。
Chapter 4 习题 (Exercises)
- 定义一个函数,接受一个平方数组(square array,一个相同维度的数组
(n n)),并将它顺时针转 90 度。
> (quarter-turn #2A((a b) (c d))) #2A((C A) (D B))
你会需要用到 361 页的 array-dimensions 。
- 阅读 368 页的
reduce说明,然后用它来定义:
(a) copy-list (b) reverse(针对列表)
- 定义一个结构来表示一棵树,其中每个节点包含某些数据及三个小孩。定义:
(a) 一个函数来复制这样的树(复制完的节点与本来的节点是不相等( `eql` )的) (b) 一个函数,接受一个对象与这样的树,如果对象与树中各节点的其中一个字段相等时,返回真。
- 定义一个函数,接受一棵二叉搜索树,并返回由此树元素所组成的,一个由大至小排序的列表。
- 定义
bst-adjoin。这个函数应与bst-insert接受相同的参数,但应该只在对象不等于任何树中对象时将其插入。
勘误: bst-adjoin 的功能与 bst-insert 一模一样。
- 任何哈希表的内容可以由关联列表(assoc-list)来描述,其中列表的元素是
(k . v)的形式,对应到哈希表中的每一个键值对。定义一个函数:
(a) 接受一个关联列表,并返回一个对应的哈希表。 (b) 接受一个哈希表,并返回一个对应的关联列表。
脚注
| [1] | 一个简单数组大小是不可调整、元素也不可替换的,并不含有填充指针(fill-pointer)。数组缺省是简单的。简单向量是个一维的简单数组,可以含有任何类型的元素。 |
| [2] | 在 ANSI Common Lisp 里,你可以给一个 :print-object 的关键字参数来取代,它只需要两个实参。也有一個宏叫做 print-unreadable-object ,能用则用,可以用 #<...> 的语法来显示对象。 |

