不知情搜索算法
不知情的搜索是一类通用搜索算法,它以强力方式运行。除了如何遍历树之外,不知情的搜索算法没有关于状态或搜索空间的附加信息,因此它也称为盲搜索。
以下是各种类型的无知搜索算法:
- 广度优先搜索
- 深度优先搜索
- 深度限制搜索
- 迭代加深深度优先搜索
- 统一成本搜索
- 双向搜索
1. 广度优先搜索
- 广度优先搜索是遍历树或图的最常见搜索策略。此算法在树或图中搜索横向,因此称为广度优先搜索。
- BFS算法从树的根节点开始搜索,并在移动到下一级节点之前扩展当前级别的所有后继节点。
- 广度优先搜索算法是通用图搜索算法的示例。
- 使用FIFO队列数据结构实现广度优先搜索。
优点:
- 如果存在任何解决方案,BFS将提供解决方案。
- 如果针对给定问题存在多个解决方案,则BFS将提供需要最少步骤的最小解决方案。
缺点:
- 它需要大量内存,因为必须将树的每个级别保存到内存中以扩展下一级别。
- 如果解决方案远离根节点,BFS需要大量时间。
示例:
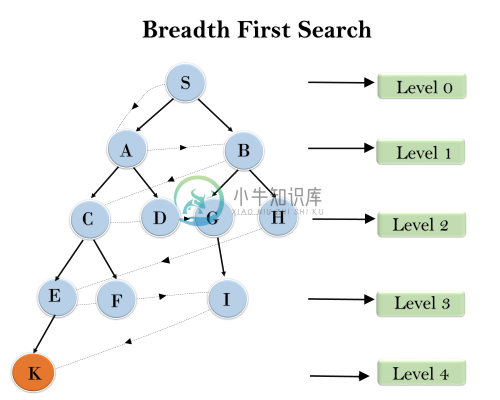
在下面的树结构中,已经显示了使用BFS算法从根节点S到目标节点K遍历树。BFS搜索算法遍历层,因此它将遵循虚线箭头所示的路径,遍历路径将是:
S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K
时间复杂度 :BFS算法的时间复杂度可以通过BFS中遍历的节点数来获得,直到最浅的节点。其中 d= 最浅解的深度,b是每个状态的节点。

空间复杂度:BFS算法的空间复杂度由边界的存储器大小O(bd)给出。
完整性:BFS完成,这意味着如果最浅的目标节点处于某个有限的深度,那么BFS将找到解决方案。
最优性:如果路径成本是节点深度的非递减函数,则BFS是最优的。
2. 深度优先搜索
- 深度优先搜索是用于遍历树或图数据结构的递归算法。
- 它从根节点开始并在移动到下一个路径之前跟随每个路径到其最大深度节点。
- DFS使用堆栈数据结构来实现它。
- DFS算法的过程类似于BFS算法。
注意:回溯是一种使用递归查找所有可能解决方案的算法技术。
优点:
- DFS需要非常少的内存,因为它只需要在从根节点到当前节点的路径上存储一堆节点。
- 到达目标节点所需的时间比BFS算法少(如果它在正确的路径中移动)。
缺点:
- 许多状态有可能继续发生,并且无法保证找到解决方案。
- DFS算法用于深入搜索,有时可能会进入无限循环。
示例
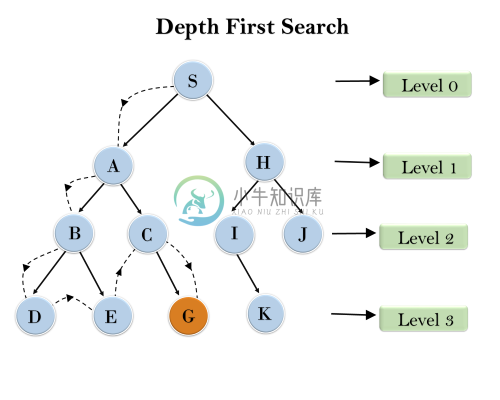
在下面的搜索树中,显示了深度优先搜索的流程,它将遵循以下顺序:
根节点 ---> 左节点 ----> 右节点
它将从根节点S开始搜索,然后遍历A,然后是B,然后是遍历E的E和E,它将回溯树,因为E没有其他后继,但仍未找到目标节点。在回溯之后,它将遍历节点C然后G,并且在此处它将在找到目标节点时终止。
完整性:DFS搜索算法在有限状态空间内完成,因为它将扩展有限搜索树中的每个节点。
时间复杂度:DFS的时间复杂度将等同于算法遍历的节点。它的公式如下:

其中,m = 任何节点的最大深度,这可能远大于d(Shallowest解算深度)
空间复杂度:DFS算法只需要存储来自根节点的单个路径,因此DFS的空间复杂度等于边缘集的大小,即O(bm)。
最佳:DFS搜索算法不是最优的,因为它可能产生大量步骤或高成本以到达目标节点。
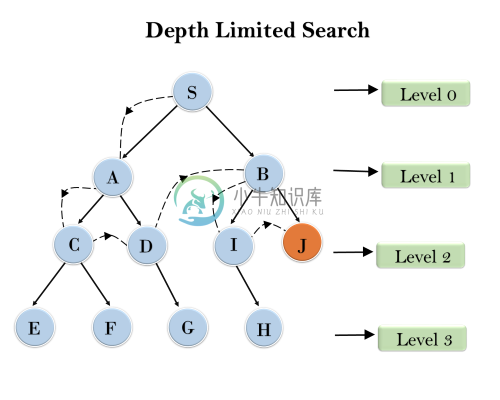
3. 深度有限搜索算法
深度有限搜索算法类似于具有预定限制的深度优先搜索。深度限制搜索可以解决深度优先搜索中无限路径的缺点。在该算法中,深度限制的节点将被视为没有后继节点。
可以使用两个失败条件终止深度限制搜索:
- 标准故障值:表示问题没有任何解决方案。
- 截止故障值:它在给定的深度限制内没有定义问题的解决方案。
优点:
- 深度限制搜索是内存高效。
缺点:
- 深度限制搜索也具有不完整性的缺点。
- 如果问题有多个解决方案,则可能不是最佳选择。
示例
- 完整性:如果解决方案高于深度限制,则DLS搜索算法完成。
- 时间复杂度:DLS算法的时间复杂度为O(bℓ)。
- 空间复杂度:DLS算法的空间复杂度为O(b×l)。
- 最佳:深度限制搜索可以看作是DFS的一个特例,即使ℓ> d也不是最优的。
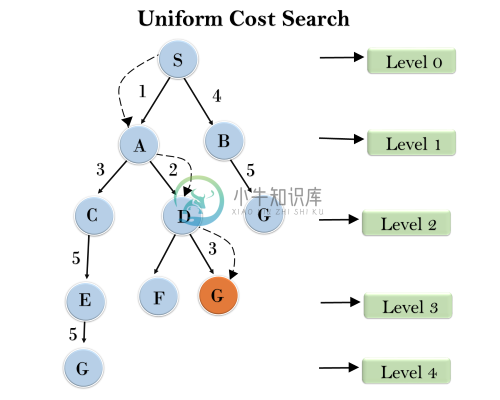
4. 统一成本搜索算法
统一成本搜索是用于遍历加权树或图的搜索算法。当每个边缘有不同的成本时,该算法开始起作用。统一成本搜索的主要目标是找到具有最低累积成本的目标节点的路径。统一成本搜索根据路径成本从根节点扩展节点。它可用于解决需要最优成本的任何图/树。统一成本搜索算法由优先级队列实现。它最优先考虑最低累积成本。如果所有边的路径成本相同,则统一成本搜索等效于BFS算法。
优点:
- 统一成本搜索是最佳的,因为在每个州都选择成本最低的路径。
缺点:
- 它不关心搜索涉及的步骤数量,只关心路径成本。由于该算法可能陷入无限循环。
示例
完整性:
统一成本搜索已经完成,例如,如果有解决方案,UCS会找到它。
时间复杂性:
设C *是最优解的成本,ε是接近目标节点的每一步。然后步数= C /ε+ 1。这里取+1,因为从状态0开始并结束为C /ε。
5. 迭代深化深度搜索
迭代深化算法是DFS和BFS算法的组合。此搜索算法找出最佳深度限制,并通过逐渐增加限制直到找到目标为止。
该算法执行深度优先搜索直到某个“深度限制”,并且在每次迭代之后它不断增加深度限制,直到找到目标节点。此搜索算法结合了广度优先搜索的快速搜索和深度优先搜索的内存效率的优势。
当搜索空间很大并且目标节点的深度未知时,迭代搜索算法对于无知搜索是有用的。
优点:
- 它结合了BFS和DFS搜索算法在快速搜索和内存效率方面的优势。
缺点:
- IDDFS的主要缺点是它重复了前一阶段的所有工作。
示例
以下树结构显示迭代加深深度优先搜索。IDDFS算法执行各种迭代,直到找不到目标节点。算法执行的迭代如下:
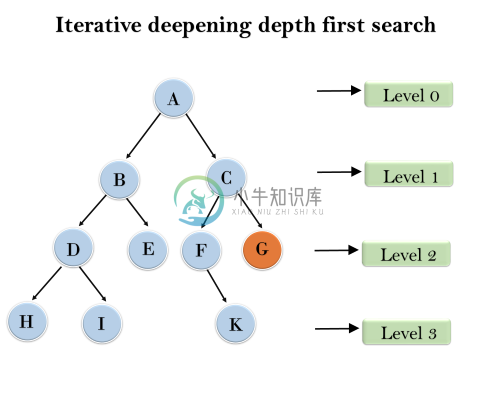
第1次迭代——-> A
第2次迭代——> A,B,C
第3次迭代———> A,B,D,E,C,F,G
第4次迭代———> A,B,D,H,I,E,C,F,K,G
在第四次迭代中,算法将找到目标节点。
完整性:
- 如果分支因子是有限的,则该算法是完整的。
时间复杂性:
- 假设b是分支因子,深度是d,那么最坏情况时间复杂度是O(bd)。
空间复杂性:
- IDDFS的空间复杂度为O(bd)。
最佳:
- 如果路径成本是节点深度的非递减函数,则IDDFS算法是最佳的。
6. 双向搜索算法
双向搜索算法运行两个同时搜索,一个形成称为前向搜索的初始状态,另一个称为后向搜索的目标节点,以找到目标节点。双向搜索用两个子图替换单个搜索图,其中一个子图从一个初始顶点开始搜索,另一个从目标顶点开始。当这两个图形相互交叉时,搜索停止。
双向搜索可以使用搜索技术,如BFS,DFS,DLS等。
优点:
- 双向搜索很快。
- 双向搜索需要更少的内存
缺点:
- 双向搜索树的实现很困难。
- 在双向搜索中,应该事先知道目标状态。
示例
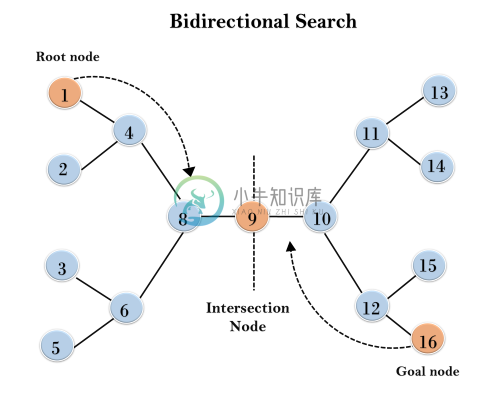
在下面的搜索树中,应用双向搜索算法。该算法将一个图/树分成两个子图。它开始在前向方向上从节点1穿过并且在向后方向上从目标节点16开始。
该算法终止于节点9,其中两个搜索相遇。
完整性: 如果我们在两次搜索中都使用BFS,则完成双向搜索。
时间复杂度: 使用BFS进行双向搜索的时间复杂度为O(b^d)。
空间复杂性: 双向搜索的空间复杂度为O(b^d)。
最佳: 双向搜索是最佳的。
