python实现Floyd算法
下面是用Python实现Floyd算法的代码,供大家参考,具体内容如下
# -*- coding: utf-8 -*-
"""
Created on Thu Jul 13 14:56:37 2017
@author: linzr
"""
## 表示无穷大
INF_val = 9999
class Floyd_Path():
def __init__(self, node, node_map, path_map):
self.node = node
self.node_map = node_map
self.node_length = len(node_map)
self.path_map = path_map
self._init_Floyd()
def __call__(self, from_node, to_node):
self.from_node = from_node
self.to_node = to_node
return self._format_path()
def _init_Floyd(self):
for k in range(self.node_length):
for i in range(self.node_length):
for j in range(self.node_length):
tmp = self.node_map[i][k] + self.node_map[k][j]
if self.node_map[i][j] > tmp:
self.node_map[i][j] = tmp
self.path_map[i][j] = self.path_map[i][k]
print '_init_Floyd is end'
def _format_path(self):
node_list = []
temp_node = self.from_node
obj_node = self.to_node
print("the shortest path is: %d")%(self.node_map[temp_node][obj_node])
node_list.append(self.node[temp_node])
while True:
node_list.append(self.node[self.path_map[temp_node][obj_node]])
temp_node = self.path_map[temp_node][obj_node]
if temp_node == obj_node:
break;
return node_list
def set_node_map(node_map, node, node_list, path_map):
for i in range(len(node)):
## 对角线为0
node_map[i][i] = 0
for x, y, val in node_list:
node_map[node.index(x)][node.index(y)] = node_map[node.index(y)][node.index(x)] = val
path_map[node.index(x)][node.index(y)] = node.index(y)
path_map[node.index(y)][node.index(x)] = node.index(x)
if __name__ == "__main__":
node = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 9), ('A', 'B', 10), ('A', 'G', 15), ('B', 'F', 2),
('G', 'F', 3), ('G', 'E', 12), ('G', 'C', 10), ('C', 'E', 1),
('E', 'D', 7)]
## node_map[i][j] 存储i到j的最短距离
node_map = [[INF_val for val in xrange(len(node))] for val in xrange(len(node))]
## path_map[i][j]=j 表示i到j的最短路径是经过顶点j
path_map = [[0 for val in xrange(len(node))] for val in xrange(len(node))]
## set node_map
set_node_map(node_map, node, node_list, path_map)
## select one node to obj node, e.g. A --> D(node[0] --> node[3])
from_node = node.index('A')
to_node = node.index('E')
Floydpath = Floyd_Path(node, node_map, path_map)
path = Floydpath(from_node, to_node)
print path
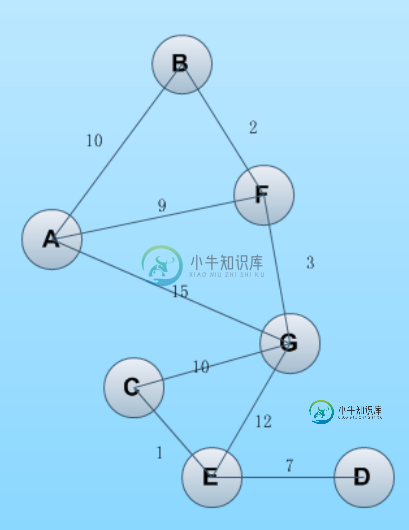
运行结果为:
the shortest path is: 23
['A', 'F', 'G', 'C', 'E']
-
一、弗洛伊德算法介绍 和Dijkstra算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。 基本思想 通过Floyd计算图G=(V,E)中各个顶点的最短路径时,需要引入一个矩阵S,矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。
-
本文向大家介绍Javascript中的Floyd-Warshall算法,包括了Javascript中的Floyd-Warshall算法的使用技巧和注意事项,需要的朋友参考一下 Djikstra的算法用于查找从一个节点到所有其他节点的最短路径的距离/路径。在某些情况下,我们需要找到从所有节点到所有其他节点的最短路径。这是所有对最短路径算法派上用场的地方。最常用的所有对最短路径算法是Floyd War
-
线性回归python实现 1.算法python代码 包含Normal Equations,批量梯度下降和随机梯度下降,这里的代码跟Logistic回归的代码类似 # -*- coding: utf-8 -*- import matplotlib.pyplot as plt import numpy as np class LinearRegression(object): def _
-
Logistic回归python实现 1.算法python代码 # -*- coding: utf-8 -*- import matplotlib.pyplot as plt import numpy as np class Logistic(object): def __init__(self): self._history_w = [] self.
-
1.python代码实现 包含算法的原始形式和对偶形式 # -*- coding: utf-8 -*- import numpy as np class Perceptron(object): def __init__(self, input_x, feature_num, input_y, learn_rate=1): self._input_x = np.arra
-
旅游规划 作者 陈越 单位 浙江大学 有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。 输入格式: 输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是
-
本文向大家介绍python实现SOM算法,包括了python实现SOM算法的使用技巧和注意事项,需要的朋友参考一下 算法简介 SOM网络是一种竞争学习型的无监督神经网络,将高维空间中相似的样本点映射到网络输出层中的邻近神经元。 训练过程简述:在接收到训练样本后,每个输出层神经元会计算该样本与自身携带的权向量之间的距离,距离最近的神经元成为竞争获胜者,称为最佳匹配单元。然后最佳匹配单元及其邻近的神经
-
本文向大家介绍python em算法的实现,包括了python em算法的实现的使用技巧和注意事项,需要的朋友参考一下 以上就是python em算法的实现的详细内容,更多关于python em算法的资料请关注呐喊教程其它相关文章!

