python 贪心算法的实现

贪心算法

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

基本思路

思想

贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止 。

步骤

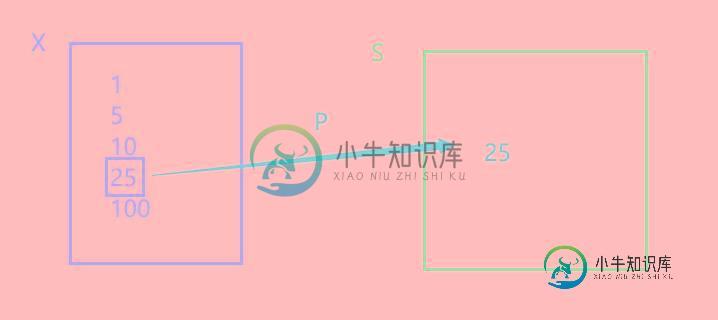
1. 遍历初始集合X中的备选元素
2. 利用贪心策略在X中确定一个元素，并将其加入到可行解S中
3. 得到可行解S

P即为贪心策略，用来选择符合条件的元素。

例子——硬币找零

假设某国硬币面值有1,5,10,25,100元五种面额，若店员为顾客找零时，需要给顾客找零a=36元，求硬币数最少的情况。

这里我们的贪心策略为：

先找到最接近a的值，然后对a进行更新，然后进行循环。

代码实现

def shortNum(a):
  coins = [1,5,10,25,100]
  out = []
  coins = coins[::-1]

  for i in coins:
    num = a//i
    out=out+[i,]*num
    a = a-num*i
    if a<=0:
      break
  return out
a = 36
print(shortNum(a))

例子——任务规划

问题描述：

输入为任务集合X= [r1,r2,r3,...,rn],每个任务ri,都对应着一个起始时间ai与结束时间bi

要求输出为最多的相容的任务集。

 如上图，r1与r2相容，r3与r1和r2都不相容。

那么这里的贪心策略我们可以设为：

1. 先将结束时间最短的任务加入到S中，
2. 再从剩下的任务的任务中选择结束时间最短的，且判断与S集合中的任务是否相容
3. 若不相容，则换下一个时间最短的任务，并进行比较
4. 循环，直至X为空。

代码实现

# 任务规划
from collections import OrderedDict
task = OrderedDict()
task['r1'] = [0,4]
task['r2'] = [5,8]
task['r3'] = [10,13]
task['r4'] = [15,18]
task['r5'] = [7,11]
task['r6'] = [2,6]
task['r7'] = [2,6]
task['r8'] = [2,6]
task['r9'] = [12,16]
task['r10'] = [12,16]
task['r11'] = [12,16]
task['r12'] = [0,3]


listTask = list(task.items())
# 根据bi进行排序，结束时间早的在前面（冒泡排序）
for i in range(len(listTask)-1):
  for j in range(len(listTask)-i-1):
    if listTask[j][1][1] > listTask[j+1][1][1]:
      listTask[j],listTask[j+1]=listTask[j+1],listTask[j]
print(listTask)
out = []
out.append(listTask.pop(0))
def isValid(temp,out):
  for k in range(len(out)):
    if temp[1][0]<out[k][1][1]:
      # 相交
      return False
  return True

for j in range(len(listTask)):
  temp = listTask.pop(0)
  # 判断是否相交
  #   相交则continue
  #   不相交则out.append(temp)
  for k in range(len(out)):
    if isValid(temp,out):
      out.append(temp)
    # else:continue 语句可以不写
    else:
      continue
print(out)

以上就是python 贪心算法的实现的详细内容，更多关于python 贪心算法的资料请关注小牛知识库其它相关文章！