Bresenham圆绘制算法的实现

Question

我已经写了一个Bresenham的圆绘制算法的实现。该算法利用了圆的高度对称特性（它只计算第一个八分之一的点，并利用对称性绘制其他点）。因此，我希望它会非常快。《图形编程黑皮书》第35章的标题是“Bresenham是快的，而且快是好的”，虽然它是关于线条绘制算法的，但我可以合理地预期圆形绘制算法也很快（因为原理是一样的）。

这是我的java，摇摆实现

public static void drawBresenhamsCircle(int r, double width, double height, Graphics g) {
    int x,y,d;
    y = r;
    x = 0;

    drawPoint(x, y, width, height,g);
    d = (3-2*(int)r);
    while (x <= y) {
        if (d <= 0) {
            d = d + (4*x + 6);
        } else {
            d = d + 4*(x-y) + 10;
            y--;
        }
        x++;

        drawPoint(x, y, width, height,g);

        drawPoint(-x, y, width, height,g);
        drawPoint(x, -y, width, height,g);

        drawPoint(-x, -y, width, height,g);
        drawPoint(y, x, width, height,g);
        drawPoint(-y, x, width, height,g);
        drawPoint(y, -x, width, height,g);

        drawPoint(-y, -x, width, height,g);
    }   
}

此方法使用以下draPoint方法：

public static void drawPoint(double x, double y,double width,double height, Graphics g) {
    double nativeX = getNativeX(x, width);
    double nativeY = getNativeY(y, height);
    g.fillRect((int)nativeX, (int)nativeY, 1, 1);
}

getNativeX和getNativeY两种方法用于将坐标从屏幕左上角的原点切换到原点位于面板中心且具有更经典轴方向的系统。

public static double getNativeX(double newX, double width) {
    return newX + (width/2);
}

public static double getNativeY(double newY, double height) {
    return (height/2) - newY;
}

我还创建了一个基于三角公式的圆绘制算法的实现（x=R*Math.cos（angle）和y=R*Math）。sin（angle））和第三个实现，使用对标准drawArc方法的调用（可在图形对象上获得）。这些附加实现的唯一目的是将Bresenham的算法与它们进行比较。

然后我创建了一些方法来画一组圆圈，以便能够很好地测量所花费的时间。下面是我使用Bresenhamhtml" target="_blank">算法绘制一组圆的方法

public static void drawABunchOfBresenhamsCircles(int numOfCircles, double width, double height, Graphics g) {
    double r = 5;
    double step = (300.0-5.0)/numOfCircles;

    for (int i = 1; i <= numOfCircles; i++) {
        drawBresenhamsCircle((int)r, width, height, g);
        r += step;
    }
}

最后，我重写了我正在使用的JPanel的绘制方法，来绘制一组圆，并测量每种类型绘制所需的时间。以下是绘制方法：

public void paint(Graphics g) {
    Graphics2D g2D = (Graphics2D)g;

    g2D.setColor(Color.RED);

    long trigoStartTime = System.currentTimeMillis();
    drawABunchOfTrigonometricalCircles(1000, this.getWidth(), this.getHeight(), g);
    long trigoEndTime = System.currentTimeMillis();
    long trigoDelta = trigoEndTime - trigoStartTime;

    g2D.setColor(Color.BLUE);

    long bresenHamsStartTime = System.currentTimeMillis();
    drawABunchOfBresenhamsCircles(1000, this.getWidth(), this.getHeight(), g);
    long bresenHamsEndTime = System.currentTimeMillis();
    long bresenDelta = bresenHamsEndTime - bresenHamsStartTime;

    g2D.setColor(Color.GREEN);

    long standardStarTime = System.currentTimeMillis();
    drawABunchOfStandardCircles(1000, this.getWidth(), this.getHeight(),g);
    long standardEndTime = System.currentTimeMillis();
    long standardDelta = standardEndTime - standardStarTime;

    System.out.println("Trigo : " + trigoDelta  + " milliseconds");
    System.out.println("Bresenham :" + bresenDelta +  " milliseconds");
    System.out.println("Standard :" + standardDelta +  " milliseconds");
}

以下是它将生成的渲染类型（每种类型绘制1000个圆）

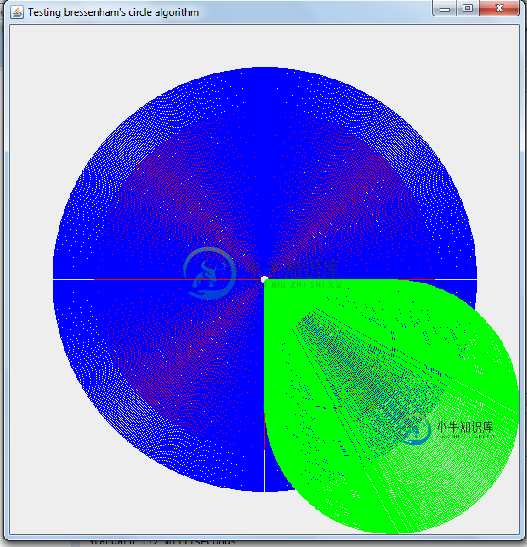
不幸的是，我的Bresenham的实现非常缓慢。我采取了许多比较措施，Bresenham的实现不仅比图形慢。drawArc，但也比三角法慢。请看以下针对不同数量圆圈的测量方法。

我的实现中哪一部分更耗时？有什么方法可以改进吗？谢谢你的帮助。

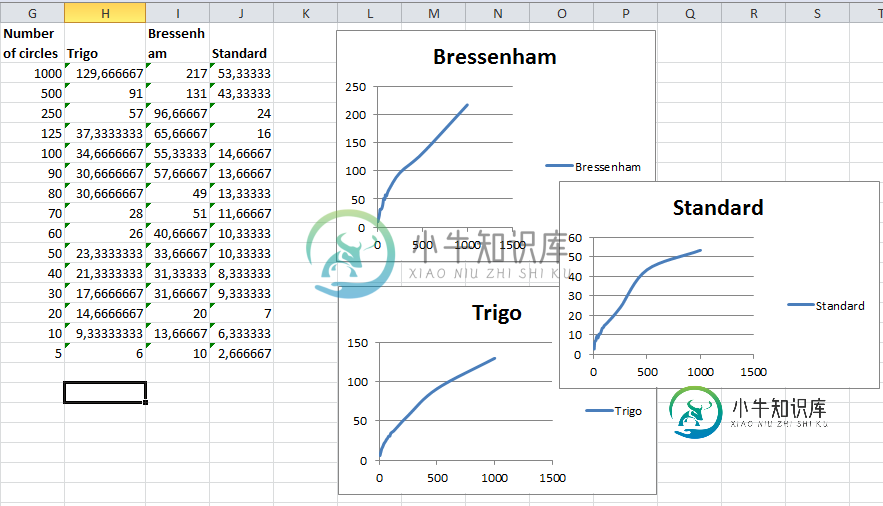
[EDITION]：根据@higuaro的要求，这是我画圆的三角算法

public static void drawTrigonometricalCircle (double r, double width, double height, Graphics g) {

    double x0 = 0;
    double y0 = 0;
    boolean isStart = true;

    for (double angle = 0; angle <= 2*Math.PI; angle = angle + Math.PI/36) {

        double x = r * Math.cos(angle);
        double y = r * Math.sin(angle);

        drawPoint((double)x, y, width, height, g);

        if (!isStart) {
            drawLine(x0,  y0, x, y, width, height, g);
        }

        isStart = false;

        x0 = x;
        y0 = y;
    }
}

以及绘制一组三角圆的方法

public static void drawABunchOfTrigonometricalCircles(int numOfCircles, double width, double height, Graphics g) {

    double r = 5;
    double step = (300.0-5.0)/numOfCircles;

    for (int i = 1; i <= numOfCircles; i++) {
        drawTrigonometricalCircle(r, width, height, g);
        r += step;
    }
}

Answer 1

最近，我自己为一个精灵光栅器编写了一个布雷森汉姆圆图实现，并试图对其进行一些优化。我不确定它会比你做的更快还是更慢，但我认为它应该有一个相当不错的执行时间。

同样不幸的是，它是用C写的。如果我明天有时间，我可能会用移植的Java版本和结果的示例图片来编辑我的答案，但现在你必须自己做，如果你愿意的话（或者其他人想花他的时间编辑它。）

基本上，它所做的是使用bresenham算法来获得圆外缘的位置，然后对圆的1/8执行该算法，并通过从中心到外缘绘制直线来镜像其余7个部分。

Color只是一个rgba值

Color* createCircleColorArray(const int radius, const Color& color, int& width, int& height) {
  // Draw circle with custom bresenham variation
  int decision = 3 - (2 * radius);
  int center_x = radius;
  int center_y = radius;
  Color* data;

  // Circle is center point plus radius in each direction high/wide
  width = height = 2 * radius + 1;
  data = new Color[width * height];

  // Initialize data array for transparency
  std::fill(data, data + width * height, Color(0.0f, 0.0f, 0.0f, 0.0f));

  // Lambda function just to draw vertical/horizontal straight lines
  auto drawLine = [&data, width, height, color] (int x1, int y1, int x2, int y2) {
    // Vertical
    if (x1 == x2) {
      if (y2 < y1) {
        std::swap(y1, y2);
      }

      for (int x = x1, y = y1; y <= y2; y++) {
        data[(y * width) + x] = color;
      }
    }

    // Horizontal
    if (y1 == y2) {
      if (x2 < x1) {
        std::swap(x1, x2);
      }

      for (int x = x1, y = y1; x <= x2; x++) {
        data[(y * width) + x] = color;
      }
    }
  };

  // Lambda function to draw actual circle split into 8 parts
  auto drawBresenham = [color, drawLine] (int center_x, int center_y, int x, int y) {
    drawLine(center_x + x, center_y + x, center_x + x, center_y + y);
    drawLine(center_x - x, center_y + x, center_x - x, center_y + y);
    drawLine(center_x + x, center_y - x, center_x + x, center_y - y);
    drawLine(center_x - x, center_y - x, center_x - x, center_y - y);
    drawLine(center_x + x, center_y + x, center_x + y, center_y + x);
    drawLine(center_x - x, center_y + x, center_x - y, center_y + x);
    drawLine(center_x + x, center_y - x, center_x + y, center_y - x);
    drawLine(center_x - x, center_y - x, center_x - y, center_y - x);
  };

  for (int x = 0, y = radius; y >= x; x++) {
    drawBresenham(center_x, center_y, x, y);

    if (decision > 0) {
      y--;
      decision += 4 * (x - y) + 10;
    }
    else {
      decision += 4 * x + 6;
    }
  }

  return data;
}

//编辑
哦，哇，我刚刚意识到这个问题有多老了。

Answer 2

你的问题在于，Bresenham的算法根据圆的大小进行可变次数的迭代，而你的三角法总是进行固定次数的迭代。

这也意味着Bresenham的算法总是会产生一个看起来平滑的圆，而你的三角方法会随着半径的增加而产生看起来更差的圆。

为了使其更加均匀，请更改三角法，以生成与Bresenham实现大致相同的点，您将看到它的速度有多快。

我编写了一些代码来对此进行基准测试，还打印了生成的点数，以下是初步结果：

三角：181毫秒，平均73分
Bresenham:120毫秒，平均867.568分

修改三角函数类以进行更多迭代以获得更平滑的圆后：

    int totalPoints = (int)Math.ceil(0.7 * r * 8);
    double delta = 2 * Math.PI / totalPoints;
    for (double angle = 0; angle <= 2*Math.PI; angle = angle + delta) {

结果如下：

三角函数：2006毫秒，平均854.933分
Bresenham：120毫秒，平均867.568分

Answer 3

你的Bresenham方法本身并不慢，只是比较慢。

Swing的drawArc（）实现依赖于机器，使用本机代码。使用Java永远无法打败它，所以不要费心尝试。（事实上，我很惊讶Java Bresenham方法与drawArc（）相比速度如此之快，这证明了执行Java字节码的虚拟机的质量。）

然而，你的三角法速度太快了，因为你没有在平等的基础上把它和布雷森汉姆进行比较。

trig方法的角度分辨率设置为PI/36（~4.7度），如for语句末尾的操作：

angle = angle + Math.PI/36  

同时，Bresenham方法依赖于半径，在每个像素变化时计算一个值。当每个八分之一点产生sqrt（2）点时，将其乘以8并除以2*Pi将获得等效的角度分辨率。因此，为了与Bresenham方法处于同等地位，您的trig方法应该具有：

resolution = 4 * r * Math.sqrt(2) / Math.PI;

在循环之外的某个地方，按如下方式为增加：

angle += resolution

由于我们现在将回到像素级分辨率，因此您实际上可以改进trig方法并删除后续的绘制线调用和对x0和y0的分配，消除不必要的转换，并进一步减少对Math的调用。以下是新方法的全部内容：

public static void drawTrigonometricalCircle (double r, double width, double height, 
    Graphics g) {

    double localPi = Math.PI;
    double resolution = 4 * r * Math.sqrt(2) / Math.PI;

    for (double angle = 0; angle <= localPi; angle += resolution) {
        double x = r * Math.cos(angle);
        double y = r * Math.sin(angle);
        drawPoint(x, y, width, height, g);
    }

}

trig方法现在执行的频率将增加几个数量级，具体取决于r的大小。

我很想看看你的结果。