Python实现EM算法实例代码
EM算法实例
通过实例可以快速了解EM算法的基本思想,具体推导请点文末链接。图a是让我们预热的,图b是EM算法的实例。
这是一个抛硬币的例子,H表示正面向上,T表示反面向上,参数θ表示正面朝上的概率。硬币有两个,A和B,硬币是有偏的。本次实验总共做了5组,每组随机选一个硬币,连续抛10次。如果知道每次抛的是哪个硬币,那么计算参数θ就非常简单了,如
下图所示:
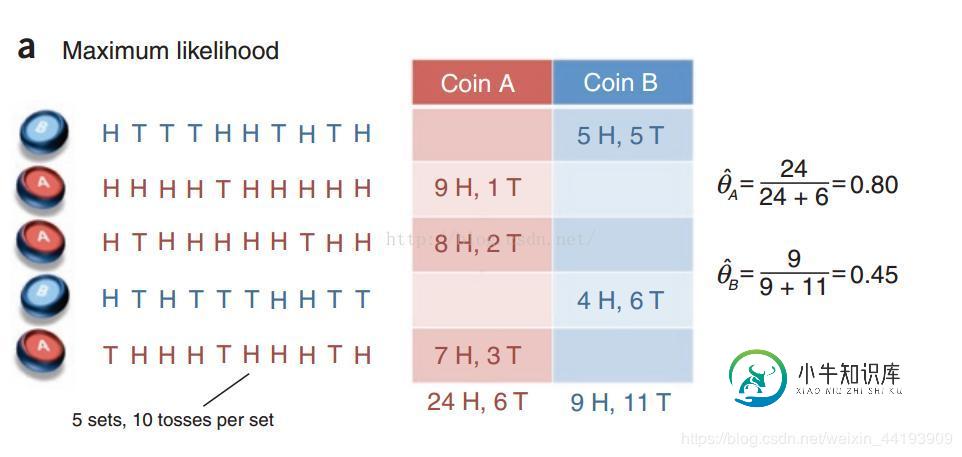
如果不知道每次抛的是哪个硬币呢?那么,我们就需要用EM算法,基本步骤为:
1、给θ_AθA和θ_BθB一个初始值;
2、(E-step)估计每组实验是硬币A的概率(本组实验是硬币B的概率=1-本组实验是硬币A的概率)。分别计算每组实验中,选择A硬币且正面朝上次数的期望值,选择B硬币且正面朝上次数的期望值;
3、(M-step)利用第三步求得的期望值重新计算θ_AθA和θ_BθB;
4、当迭代到一定次数,或者算法收敛到一定精度,结束算法,否则,回到第2步。

计算过程详解:初始值θ_A^{(0)}θA(0)=0.6,θ_B^{(0)}θB(0)=0.5。
由两个硬币的初始值0.6和0.5,容易得出投掷出5正5反的概率是p_A=C^5_{10}*(0.6^5)*(0.4^5)pA=C105∗(0.65)∗(0.45),p_B=C_{10}^5*(0.5^5)*(0.5^5)pB=C105∗(0.55)∗(0.55), p_ApA/(p_ApA+p_BpB)=0.449, 0.45就是0.449近似而来的,表示第一组实验选择的硬币是A的概率为0.45。然后,0.449 * 5H = 2.2H ,0.449 * 5T = 2.2T ,表示第一组实验选择A硬币且正面朝上次数和反面朝上次数的期望值都是2.2,其他的值依次类推。最后,求出θ_A^{(1)}θA(1)=0.71,θ_B^{(1)}θB(1)=0.58。重复上述过程,不断迭代,直到算法收敛到一定精度为止。
这篇博客对EM算法的推导非常详细,链接如下:
https://blog.csdn.net/zhihua_oba/article/details/73776553
Python实现
#coding=utf-8
from numpy import *
from scipy import stats
import time
start = time.perf_counter()
def em_single(priors,observations):
"""
EM算法的单次迭代
Arguments
------------
priors:[theta_A,theta_B]
observation:[m X n matrix]
Returns
---------------
new_priors:[new_theta_A,new_theta_B]
:param priors:
:param observations:
:return:
"""
counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
theta_A = priors[0]
theta_B = priors[1]
#E step
for observation in observations:
len_observation = len(observation)
num_heads = observation.sum()
num_tails = len_observation-num_heads
#二项分布求解公式
contribution_A = stats.binom.pmf(num_heads,len_observation,theta_A)
contribution_B = stats.binom.pmf(num_heads,len_observation,theta_B)
weight_A = contribution_A / (contribution_A + contribution_B)
weight_B = contribution_B / (contribution_A + contribution_B)
#更新在当前参数下A,B硬币产生的正反面次数
counts['A']['H'] += weight_A * num_heads
counts['A']['T'] += weight_A * num_tails
counts['B']['H'] += weight_B * num_heads
counts['B']['T'] += weight_B * num_tails
# M step
new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
return [new_theta_A,new_theta_B]
def em(observations,prior,tol = 1e-6,iterations=10000):
"""
EM算法
:param observations :观测数据
:param prior:模型初值
:param tol:迭代结束阈值
:param iterations:最大迭代次数
:return:局部最优的模型参数
"""
iteration = 0;
while iteration < iterations:
new_prior = em_single(prior,observations)
delta_change = abs(prior[0]-new_prior[0])
if delta_change < tol:
break
else:
prior = new_prior
iteration +=1
return [new_prior,iteration]
#硬币投掷结果
observations = array([[1,0,0,0,1,1,0,1,0,1],
[1,1,1,1,0,1,1,1,0,1],
[1,0,1,1,1,1,1,0,1,1],
[1,0,1,0,0,0,1,1,0,0],
[0,1,1,1,0,1,1,1,0,1]])
print (em(observations,[0.6,0.5]))
end = time.perf_counter()
print('Running time: %f seconds'%(end-start))
总结
到此这篇关于Python实现EM算法实例的文章就介绍到这了,更多相关Python实现EM算法实例内容请搜索小牛知识库以前的文章或继续浏览下面的相关文章希望大家以后多多支持小牛知识库!
-
本文向大家介绍python em算法的实现,包括了python em算法的实现的使用技巧和注意事项,需要的朋友参考一下 以上就是python em算法的实现的详细内容,更多关于python em算法的资料请关注呐喊教程其它相关文章!
-
本文向大家介绍python实现kmp算法的实例代码,包括了python实现kmp算法的实例代码的使用技巧和注意事项,需要的朋友参考一下 kmp算法 kmp算法用于字符串的模式匹配,也就是找到模式字符串在目标字符串的第一次出现的位置 比如 abababc 那么bab在其位置1处,bc在其位置5处 我们首先想到的最简单的办法就是蛮力的一个字符一个字符的匹配,但那样的时间复杂度会是O(m*n) kmp算
-
本文向大家介绍Python实现搜索算法的实例代码,包括了Python实现搜索算法的实例代码的使用技巧和注意事项,需要的朋友参考一下 将数据存储在不同的数据结构中时,搜索是非常基本的必需条件。最简单的方法是遍历数据结构中的每个元素,并将其与您正在搜索的值进行匹配。这就是所谓的线性搜索。它效率低下,很少使用,但为它创建一个程序给出了我们如何实现一些高级搜索算法的想法。 线性搜索 在这种类型的搜索中,逐
-
本文向大家介绍python实现数独算法实例,包括了python实现数独算法实例的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了python实现数独算法的方法。分享给大家供大家参考。具体如下: 希望本文所述对大家的Python程序设计有所帮助。
-
本文向大家介绍Python排序算法实例代码,包括了Python排序算法实例代码的使用技巧和注意事项,需要的朋友参考一下 排序算法,下面算法均是使用Python实现: 插入排序 原理:循环一次就移动一次元素到数组中正确的位置,通常使用在长度较小的数组的情况以及作为其它复杂排序算法的一部分,比如mergesort或quicksort。时间复杂度为 O(n2) 。 选择排序 原理:每一趟都选择最小的值和
-
本文向大家介绍Python实现KNN(K-近邻)算法的示例代码,包括了Python实现KNN(K-近邻)算法的示例代码的使用技巧和注意事项,需要的朋友参考一下 一、概述 KNN(K-最近邻)算法是相对比较简单的机器学习算法之一,它主要用于对事物进行分类。用比较官方的话来说就是:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例, 这K个实例的多数属于某个类,就把该输入实

