Python随机生成均匀分布在三角形内或者任意多边形内的点

Python有一随机函数可以产生[0,1)区间内的随机数，基于此函数生成随机分布在任意三角形内的点
由数学知识得知：
几何体的向量表达形式

直线：

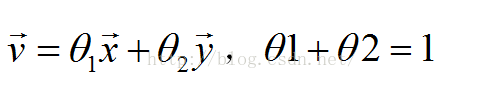
线段：

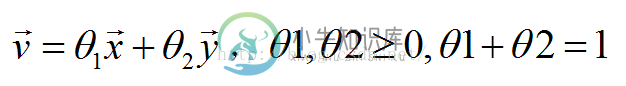
推广到高维

三维平面：

三角形：

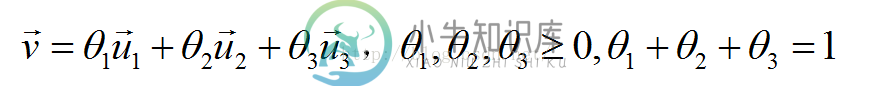
注释，v这个向量表示的是在图形上的点的坐标，根据数学知识得知，直线和三维平面内的v构成的点集是放射集，而线段则是凸集， 其余向量是不在同一个点或者同一个平面的点的坐标构成的列向量
那么针对三角形可以写成如下：

我们可以先生成随机的贝塔，然后随机生成阿尔法，然后处理阿尔法，使得点是随机落在三角形内的，这里用的是开始生成的随机数的算术平方根作为阿尔法数值，关于为什么这样可以参考
Python随机生成均匀分布在单位圆内的点

现附代码如下：

import numpy as np 
import matplotlib.pyplot as plt 
 
if __name__ == '__main__': 
 x1, y1 = 0, 30 
 x3, y3 = 200, -10 
 x2, y2 = 100, 200 
 sample_size = 500 
 theta = np.arange(0,1,0.001) 
 x = theta * x1 + (1 - theta) * x2 
 y = theta * y1 + (1 - theta) * y2 
 plt.plot(x,y,'g--',linewidth=2) 
 x = theta * x1 + (1 - theta) * x3 
 y = theta * y1 + (1 - theta) * y3 
 plt.plot(x, y, 'g--', linewidth=2) 
 x = theta * x2 + (1 - theta) * x3 
 y = theta * y2 + (1 - theta) * y3 
 plt.plot(x, y, 'g--', linewidth=2) 
 rnd1 = np.random.random(size = sample_size) 
 rnd2 = np.random.random(size=sample_size) 
 rnd2 = np.sqrt(rnd2) 
 x = rnd2 * (rnd1 * x1 + (1 - rnd1) * x2) + (1 - rnd2) * x3 
 y = rnd2 * (rnd1 * y1 + (1 - rnd1) * y2) + (1 - rnd2) * y3 
 plt.plot(x,y,'ro') 
 plt.grid(True) 
 # plt.savefig('demo.png') 
 plt.show()

生成图：

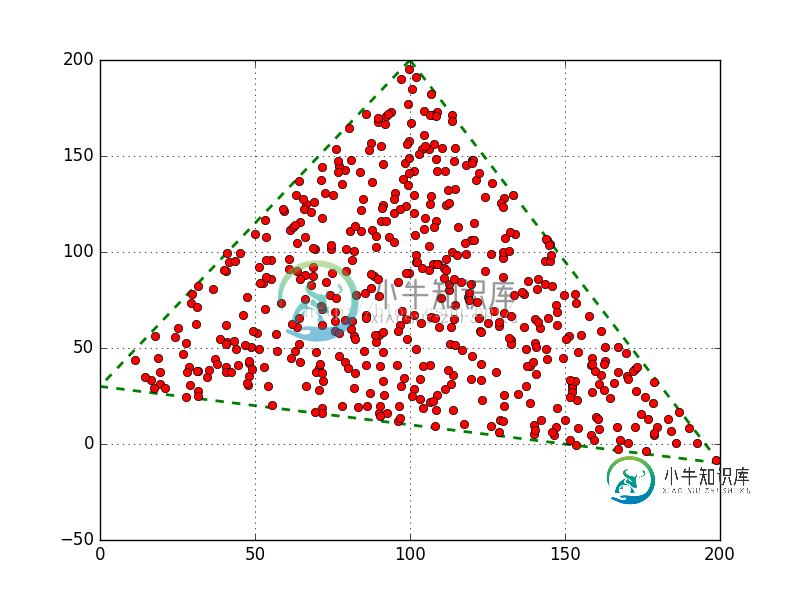
作为推广，其实多个多边形也是可以这样生成的，只需要分割为多个三角形，根据三角形面积比例，控制样本比例即可。

 以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。