C#递归算法之分而治之策略

1.分而治之的概念    

　　分而治之是一种使用递归解决问题的算法，主要的技巧是将一个大的复杂的问题划分为多个子问题，而这些子问题可以作为终止条件，或者在一个递归步骤中得到解决，所有子问题的解决结合起来就构成了对原问题的解决

2.分而治之的优点和缺点

　　分而治之算法通常包括一个或者多个递归方法的调用，当这些调用将数据分隔成为独立的集合从而处理较小集合的时候，分而治之的策略将会有很高的效率，而在数据进行分解的时候，分而治之的策略可能会产生大量的重复计算，从而导致性能的降低。

3.画标尺程序的分析讲解

　　画标尺是分而治之的策略的一个简单应用，标尺是由长度为1英寸的单元构成的序列，每个单元的末端有最长的记号，每个寸单元的1/2英寸处的记号要比末端的短，在1/4处的记号比1/2的要短，1/8处比1/4处短，编写一个程序，在一条线上，用规则间隔来绘制标记，在特定位置有特定大小的记号。

　　分析：在一个直线上，我们可以首先将这条直线一分为二,然后对分出来的二个再进行拆分。直到满足一定的精度要求，比如以最小刻度为1/8英寸为例，drawRuler作为画标尺的第归函数，在drawRuler函数中用一段线段的两端(起点（startPos），终点(endPos))，和变量h作为参数,标记的基础高度为baseHeight，而标记的高度应该为h*baseHeight,则标尺的画法可以分析如下：

　　计算间隔（0.0，1.0）的中点：midPos = (startPost+endPos)/2;在中点1/2处画一个标记，高度为3*baseHeight

　　将中点分隔开的为两条直线，再使用第归函数drawRule，对应的起点，终点为（0.0，0.5）和(0.5,1.0)，参数h-1,这样可以使高度相比短些

　　第归步骤2（h＝2）

　　midPos = (0.0+0.5)/2   (1/4处)，高度为 2*baseHeight

　　midPos = (0.5+1.0)/2   (3/4处）高度为 2*baseHeight

　　第归步骤（h=1）

　　分别在1/8处和7/8处标记，计算方法

　　midPos = (0.0+0.25)/2  (1/8)    高度为baseHeight

　　midPos = (0.75+1)/2  (7/8)     高度为baseHeight

　　用图示可以表示如下

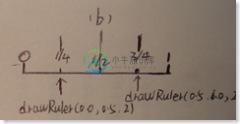
　　我们可以将连续第归产生的记号看作二叉树的节点。树根h为初值。就是1/2处的记号，每个父记号都产生了两个子记号。如下图所示

4.可执行程序文件

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Text;
using System.Windows.Forms;

namespace DrawRuler
{
 public partial class Form1 : Form
 {
 public Form1()
 {
 InitializeComponent();
 }

 private void Form1_Load(object sender, EventArgs e)
 {
 }

 void drawRuler(float startPos, float endPos, int h)
 {
 float baseHeight =4;
 if (h > 0)
 {
 float midPos = (startPos + endPos) / 2;
 float height = h * baseHeight;
 drawMark(midPos, height);
 drawRuler(startPos, midPos, h - 1);
 drawRuler(midPos, endPos, h - 1);
 }
 }

 void drawMark(float pos, float height)
 {
 using (Graphics g = this.CreateGraphics())
 {
 float xOffset = 100 + pos;
 float yOffset = 100-height;
 SolidBrush brusuh = new SolidBrush(Color.Black);
 Pen p = new Pen(brusuh, 1);
 g.DrawLine(p, xOffset, yOffset, xOffset, 100);
 }
 }
 private void Form1_Paint(object sender, PaintEventArgs e)
 {
 #region 首先画一条直线
 using (Graphics g = e.Graphics)
 {
 float xOffset = 100;
 float yOffset = 100;
 int len = 300;
 SolidBrush brusuh = new SolidBrush(Color.Black);
 Pen p = new Pen(brusuh, 2);
 g.DrawLine(p, xOffset, yOffset, xOffset + len, yOffset);
 }
 #endregion

 drawRuler(0, 300, 3);
 }
 }
}

5.代码下载
http://xiazai.jb51.net/201606/yuanma/DrawRuler(jb51.net).rar

以上就是本文的全部内容，希望能给大家一个参考，也希望大家多多支持小牛知识库。