C#函数式编程中的递归调用之尾递归详解

关于递归相信大家已经熟悉的不能再熟悉了，所以笔者在这里就不多费口舌，不懂的读者们可以在博客园中找到很多与之相关的博客。下面我们直接切入正题，开始介绍尾递归。

尾递归

普通递归和尾递归如果仅仅只是从代码的角度出发来看，我们可能发现不了他的特点，所以笔者利用两张堆栈上的图来展示具体的差距在哪，首先我们来看看普通的递归调用的情况，如下图1.1所示：

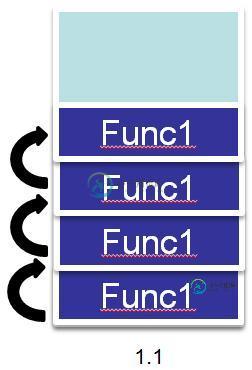
假设这里执行的函数是Func1，并且Func1中通过递归调用了自己，那么我们可以看到栈上在每次调用Func1的时候都会重新将函数返回地址等其他参数放入栈中，在递归次数较少的情况下，这样是不会有问题的。但如果递归调用次数达到一定的数量级，则会将栈空间消耗光。因此，就提出了尾递归。而尾递归的栈图如1.2所示：

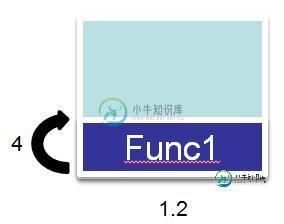
一样还是递归，但是每次执行自身的时候并不会在栈空间中申请新的空间，类似于for循环的效果，面对递归次数很多的情况下也不会出现什么问题。但是新的问题就出来了，在C#中编译器不会做到这一步优化，而是在jit编译器执行时才会进行优化。并且只有64位才进行优化。在语言的层面上我们也要遵守一定的原则，才能让编译器知道去优化。当然有些喜欢看博客的人可能早就知道尾递归就是在最后return的时候调用自身。我们可以通过一串示意代码来看尾调用：

int Func1()

{

  return Func1();

}

当然上面这串代码会形成一个死循环，因为这里我们没有基线条件。下面我们举一个例子：

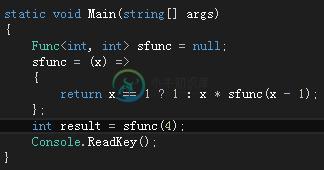
这个函数想必应该会比较熟悉，就是计算阶乘的。但是我们可以发现函数sunfc最后的返回语句并不是直接调用函数本身，而是x*sfunc(x -1)，恰恰就是因为前面这个x*就会导致编译器无法优化，从而只能采用普通的递归调用的方式去执行，那么我们就需要利用一些模式去改变，首先我们先介绍的是“累加器传递模式”，可能名字比较悬乎，其实就是将当前的计算结果传递给下一次调用函数中，这样当到达基线条件后直接根据上次计算的结果算出最终结果返回即可，如果将上面的代码采用这个模式就是下面这个样子：

采用这个模式之后我们就变回了尾递归了，当执行到基线条件时，直接返回y的值即可。根本不需要回溯到以前。除了利用这种模式，我们还可以利用一种“后继传递模式”，跟累加器传递模式一样也需要修改函数签名，增加一个参数，我们继续修改上面这串代码：

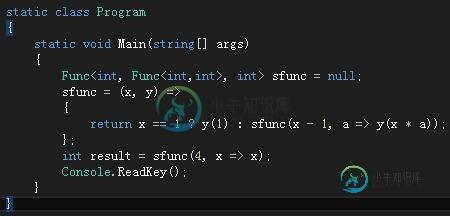
相比累加器传递模式，这种方式比较难理解，其实sfunc在到达基线条件时y就等同于下面这个lambda表达式：a => a*4*3*2，然后就是调用y(1)就直接计算最终的结果了。在简单点就是y这个函数被包装了了好几层，比如上面这段函数执行结束时y的调用顺序：

a为1传递给y(2 * a)，结果就是y(2)。

a为2传递给y(3 * a)，结果就是y(6)。

a为6传递给y(4 * a)，结果就是y(24)。

a为24传递给x => x，输出24。

如果还是不理解只能下断点，调试自己琢磨琢磨了，实在不懂的可以Q问。

在满足必要的经济的条件下,研究更加高深的技术.满足自己的野心