分而治之的占优点计数算法?
假设坐标(x1,y1)上的一个点支配另一个点(x2,y2)如果x1≤x2,y1≤y2;
我有一组点(x1,y1),...(xn,yn),我想找到支配对的总数。我可以通过比较所有点来使用蛮力,但这需要时间O(n2)。相反,我想使用分而治之的方法在时间O(n log n)中解决这个问题。
现在,我有以下算法:
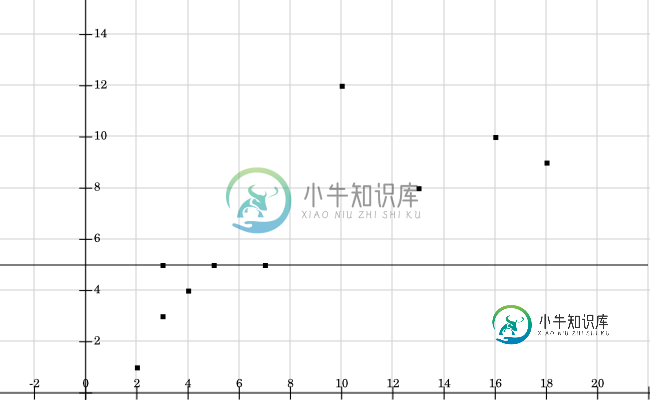
所以y坐标的两个半部分是:{1,3,4,5,5}和{5,8,9,10,12}
我画分界线。
共有1个答案
假设您按照y坐标的升序分别对两个一半中的点进行排序。现在,看看两半中的最低y值点。如果左边的最低点的y值比右边的最低点低,那么那个点是由右边的所有点支配的。否则,右边的底点并不能支配左边的任何东西。
在任何一种情况下,您都可以从两个一半中的一个中删除一点,并对剩余的排序列表重复该过程。这对每个点起O(1)的作用,所以如果有n个总点,这对(排序后)起O(n)的作用,以计算两个一半上的支配对的数量。如果您以前见过,这类似于数组中的反向计数算法)。
将对点进行排序所需的时间(O(n log n))进行分解,这个征服步骤需要O(n log n)时间,给出了一个递归
T(n)=2T(n/2)+O(n log n)
这根据主定理求解为O(nlog2n)。
但是,您可以加快速度。假设在开始分治步骤之前,通过点的y坐标预置点,做一遍O(n log n)工作。使用类似于最接近点对问题的技巧,您可以在大小为n的每个子问题上以O(n)时间排序每一半的点(有关详细信息,请参阅本页底部的讨论)。这将循环更改为
-
本文向大家介绍C#递归算法之分而治之策略,包括了C#递归算法之分而治之策略的使用技巧和注意事项,需要的朋友参考一下 1.分而治之的概念 分而治之是一种使用递归解决问题的算法,主要的技巧是将一个大的复杂的问题划分为多个子问题,而这些子问题可以作为终止条件,或者在一个递归步骤中得到解决,所有子问题的解决结合起来就构成了对原问题的解决 2.分而治之的优点和缺点 分而治之算法通常包括一个或
-
我必须在C++中为函数实现分治算法,该函数返回数组中的最大值。我理解算法并已经设计了函数,但我遇到了数组索引的问题。 在伪代码中,下面是我的函数: 有没有办法找到这些导致正确行为的指数?我很感激你的帮助。
-
在分而治之的方法中,手头的问题被分成较小的子问题,然后每个问题都独立解决。 当我们继续将子问题划分为更小的子问题时,我们最终可能会达到无法进行更多划分的阶段。 解决那些“原子”最小可能的子问题(分数)。 最后合并所有子问题的解决方案以获得原始问题的解决方案。 从广义上讲,我们可以通过三个步骤来理解divide-and-conquer方法。 Divide/Break 此步骤涉及将问题分解为更小的子问
-
我和朋友在讨论是否可以在不排序数组的情况下,使用分治算法计算数组a[1…n]中出现的某个元素k的数量? 我们遇到了一个障碍,如果我们使用二进制搜索,一旦找到元素,它就会停止。有什么想法吗?
-
我正在纠结于分治算法对于大于2的维度是如何工作的,特别是如何在两个子问题之间找到最接近的点对。 我知道在3D的情况下,我需要将每个点与其他15个点进行比较。 我不明白的是,那15点怎么选?在2D情况下,只需按值对值进行排序,然后按顺序进行遍历。然而,在3D情况下,每个点都需要与和轴上离它最近的15个点进行比较。我似乎找不到一种方法来确定这15个点是什么,而且不存在... 我错过了什么?
-
主要内容:分治算法的利弊,分治算法的应用场景实际场景中,我们之所以觉得有些问题很难解决,主要原因是该问题涉及到大量的数据,如果只需要处理少量的数据,问题会变得非常容易解决。 举一个简单的例子,设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说,直接实现对 1000 个整数进行排序是非常困难的。而同样的问题,如果转换成对 2 个整数进行排序,解决起来就很容易。 分治算法中,“分治”即“分而治之”的意思。分治算法

