《深圳昂楷》专题
-
 深入理解python中的闭包和装饰器
深入理解python中的闭包和装饰器本文向大家介绍深入理解python中的闭包和装饰器,包括了深入理解python中的闭包和装饰器的使用技巧和注意事项,需要的朋友参考一下 python中的闭包从表现形式上定义(解释)为:如果在一个内部函数里,对在外部作用域(但不是在全局作用域)的变量进行引用,那么内部函数就被认为是闭包(closure)。 以下说明主要针对 python2.7,其他版本可能存在差异。 也许直接看定义并不太能明白,下面
-
深入浅析Vue.js中 computed和methods不同机制
本文向大家介绍深入浅析Vue.js中 computed和methods不同机制,包括了深入浅析Vue.js中 computed和methods不同机制的使用技巧和注意事项,需要的朋友参考一下 在vue.js中,有methods和computed两种方式来动态当作方法来用的 1.首先最明显的不同 就是调用的时候,methods要加上() 2.我们可以使用 methods 来替代 computed,效
-
递归深度受限制的旅行目录树
问题内容: 我需要递归处理目录树中的所有文件,但是深度有限。 例如,这意味着要在当前目录和前两个子目录级别中查找文件,但不能再查找任何文件。在这种情况下,我必须处理,但不能处理。 我将如何在Python 3中做到最好? 目前,我使用这样的循环来处理所有文件直至无限深度: 我可以想到一种计数目录分隔符()的方法,以确定当前文件的层次级别,如果该级别超过所需的最大值,则确定循环。 当存在大量要忽略的子
-
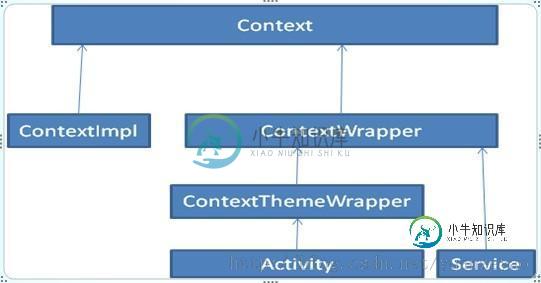 深入解析Android App开发中Context的用法
深入解析Android App开发中Context的用法本文向大家介绍深入解析Android App开发中Context的用法,包括了深入解析Android App开发中Context的用法的使用技巧和注意事项,需要的朋友参考一下 Context在开发Android应用的过程中扮演着非常重要的角色,比如启动一个Activity需要使用context.startActivity方法,将一个xml文件转换为一个View对象也需要使用Context对象,可以
-
用于深度嵌套JSON的Cloudant / Mango选择器
问题内容: 假设我的一些文档具有以下结构: 是否有MangoJSON选择器可以成功选择值?它在数组内部(我知道它在数组中的位置)。我也对过滤结果感兴趣,所以我只能得到结果。 我已经尝试了很多东西,包括$ elemMatch,但是所有东西大多数都返回“无效的json”。 那是芒果的用例还是我应该坚持观点? 问题答案: 使用Cloudant Query(Mango)选择器语句,您仍然需要在查询之前定义
-
深入剖析JavaScript中的函数currying柯里化
本文向大家介绍深入剖析JavaScript中的函数currying柯里化,包括了深入剖析JavaScript中的函数currying柯里化的使用技巧和注意事项,需要的朋友参考一下 curry化来源与数学家 Haskell Curry的名字 (编程语言 Haskell也是以他的名字命名)。 柯里化通常也称部分求值,其含义是给函数分步传递参数,每次传递参数后部分应用参数,并返回一个更具体的函数接受
-
 JS XMLHttpRequest原理与使用方法深入详解
JS XMLHttpRequest原理与使用方法深入详解本文向大家介绍JS XMLHttpRequest原理与使用方法深入详解,包括了JS XMLHttpRequest原理与使用方法深入详解的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了JS XMLHttpRequest原理与使用方法。分享给大家供大家参考,具体如下: 你真的会使用XMLHttpRequest吗? 看到标题时,有些同学可能会想:“我已经用xhr成功地发过很多个Ajax请求了,对
-
深拷贝里的循环引用如何解决?
本文向大家介绍深拷贝里的循环引用如何解决?相关面试题,主要包含被问及深拷贝里的循环引用如何解决?时的应答技巧和注意事项,需要的朋友参考一下 考察的是如何实现深拷贝问题。深拷贝需要为每一个对象属性创建新的对象,但是如果单纯这样做碰到含有循环引用的对象,就会进入死循环。 这么操作当然是错误的,为了正确进行深拷贝,不出现这种错误,就需要: 遍历原对象每个节点的时候,记录该节点是否被访问过,这样当在遍历过
-
Java Builder模式和“深层”对象层次结构
问题内容: 在“深度”对象层次结构中使用Builder模式的最佳实践是什么?详细地说,我探讨了将Joshua Bloch提出的Builder模式应用于我的XML绑定代码的想法(我使用的是SimpleXML,但是这个问题将适用于任何情况)。我的对象层次结构深达4个级别,具有不同程度的复杂性。我的意思是,在某些级别上,我的对象只有几个属性,而在其他级别上,我最多可以有10个属性。 因此,请考虑以下假设
-
为什么JVM具有最大的内联深度?
问题内容: 有一个参数(默认值为9),该参数控制对内联的嵌套调用的最大数量。为什么会有这样的限制?为什么基于频率和代码大小的常规启发式方法不足以使JVM自行决定内联的深度? (这是由JitWatch提示的,向我显示了由于深度而未内嵌深层嵌套的Guava 调用) 问题答案: 一些重要的搜索发现了这个有趣的小片段(我实际上到达了Google搜索的第 4 页): 这表明,按预期的那样,硬限制是您停止内联
-
Python: 浅拷贝与深拷贝的区别说明?
浅复制 将对象的引用存储在新的内存位置。对新位置所做的更改也会反映在以前的位置上。它比深拷贝更快。 深度复制 将对象的值存储在新位置。对新位置所做的任何更改都不会反映在以前的位置上。id 用于查看对象的内存地址。当然,下面例子的地址在你的计算机上是不同的。 ## 浅拷贝 data = [1, 2, 3, 4, 5] updated_data = data updated_data.
-
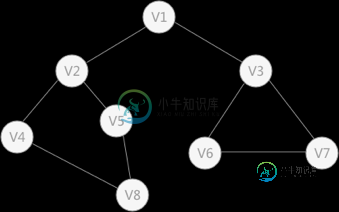 深度优先搜索和广度优先搜索
深度优先搜索和广度优先搜索主要内容:深度优先搜索(简称“深搜”或DFS),广度优先搜索,总结前边介绍了有关图的 4 种存储方式,本节介绍如何对存储的图中的顶点进行遍历。常用的遍历方式有两种: 深度优先搜索和 广度优先搜索。 深度优先搜索(简称“深搜”或DFS) 图 1 无向图 深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。例如图 1 是一个无向图,采用深度优先算法遍历这个图的过程为: 首先任意找一个未被遍历过的顶点,例如从 V1 开始,由于 V1 率先访问过了,所以
-
最小极大算法不适用于深度>1
我正在 python 上做一个棋盘游戏,我需要在其中实现算法最小值。当我尝试增加搜索深度时,我的程序停止工作。我也尝试实施 alpha beta 削减,但它似乎无法正常工作。当我尝试其他深度值时,它开始进行无效播放,并且还出现此错误: 以下是我的代码: 阿尔法测试版修剪: 辅助功能: 启发式功能:
-
JAVA-打印二叉查找树的节点深度
我试图打印我的二叉搜索树的每个节点的所有值和深度。我很难想出一种递归计算深度的方法。到目前为止,我有一种仅打印树的每个值的方法。我将不胜感激一些指导,因为我觉得我让它变得比应有的更难。
-
递归查找二叉树中节点的深度
我坚持使用递归函数来查找二叉树中节点的深度,更具体地说,是在else条件中: 如果树是二叉搜索树,知道左子值总是低于父值,右子值总是高于父值,我可以添加一个If条件,这样如果节点x值低于根,我总是返回根- 当查看函数时,假设节点总是存在的,节点x永远不是根,并且在开始时传递的深度总是0。 如果树是二叉搜索:
