《算法》专题
-
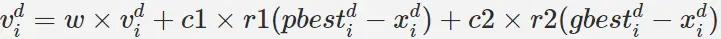 python实现粒子群算法
python实现粒子群算法本文向大家介绍python实现粒子群算法,包括了python实现粒子群算法的使用技巧和注意事项,需要的朋友参考一下 粒子群算法 粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。CAS理论于1994年正式提出,CAS中的成员称为主体。比如研究鸟群系统,每个鸟在这个系统中就称为主体。主体有适应性,它能够与环境及其他的主体进行交流,并且根据交流的过程“学习”或“积累
-
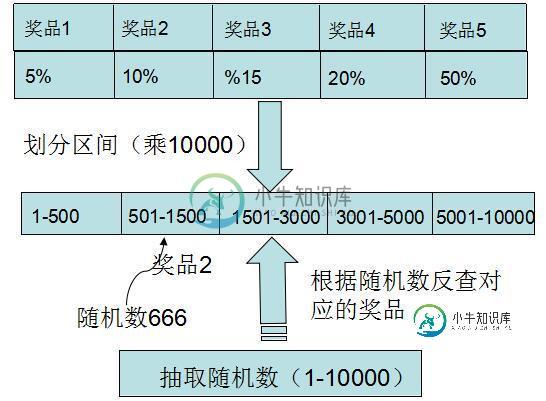 Java抽奖算法第二例
Java抽奖算法第二例本文向大家介绍Java抽奖算法第二例,包括了Java抽奖算法第二例的使用技巧和注意事项,需要的朋友参考一下 本文实例为大家分享了java抽奖算法,供大家参考,具体内容如下 1. 算法分析 根据概率将奖品划分区间,每个区间代表一个奖品,然后抽取随机数,反查落在那个区间上,即为所抽取的奖品。 2. 代码 核心算法 Prize bean 3. 测试 prize1概率: 5% prize2概率:
-
 循环调度算法示例
循环调度算法示例在以下示例中,有六个进程分别命名为P1,P2,P3,P4,P5和P6。 他们的到达时间和爆发时间如下表所示。 系统的时间量是4个单位。 进程ID 到达时间 突发时间 1 0 5 2 1 6 3 2 3 4 3 1 5 4 5 6 6 4 根据算法,我们必须保持就绪队列和甘特图。 两个数据结构的结构在每次调度后都会改变。 就绪队列: 最初,在时间,过程P1到达,其将被安排为时间片4单位。 因此,在就
-
操作系统调度算法
操作系统使用各种算法来有效地调度处理器上的进程。 调度算法的目的 最大CPU利用率 公平分配CPU 最大吞吐量 最短周转时间 最短的等待时间 最短响应时间 有以下算法可用于计划作业。 1. 先来先服务 这是最简单的算法。 最短到达时间的过程将首先获得CPU。 到达时间越少,进程得到CPU的速度越快。 这是非抢先式的调度。 2. 轮循 在循环调度算法中,操作系统定义了一个时间片(片)。 所有的进程将
-
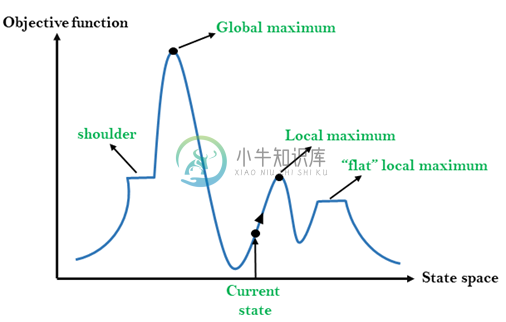 人工智能爬山算法
人工智能爬山算法主要内容:爬山算法的特点,爬山的国家空间图,状态的不同区域,爬山类型算法:,爬山算法存在的问题爬山(Hill Climbing)算法是一种局部搜索算法,它在增加高度/值的方向上连续移动,以找到山峰或最佳解决问题的方法。它在达到峰值时终止,其中没有邻居具有更高的值。 爬山算法是一种用于优化数学问题的技术。其中一个广泛讨论的爬山算法的例子是旅行商问题,其中我们需要最小化推销员的行进距离。 它也称为贪婪的本地搜索,因为它只关注其良好的直接邻居状态而不是超越它。爬山算法的节点有两个组成部分,即状态
-
 人工智能搜索算法
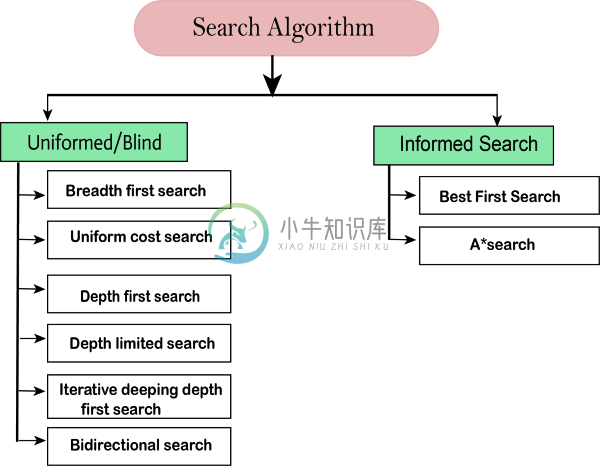
人工智能搜索算法主要内容:解决问题的代理,搜索算法术语,搜索算法的属性,搜索算法的类型搜索算法是人工智能最重要的领域之一。本主题将解释有关AI中搜索算法的所有信息。 解决问题的代理 在人工智能中,搜索技术是普遍的问题解决方法。AI中的合理代理或问题解决代理主要使用这些搜索策略或算法来解决特定问题并提供最佳结果。解决问题的代理是基于目标的代理并使用原子表示。在本主题中,我们将学习各种解决问题的搜索算法。 搜索算法术语 搜索:搜索是一个一步一步的过程,用于解决给定搜索空间中的搜索问题。
-
sklearn决策树分类算法
主要内容:决策树算法应用,决策树实现步骤,决策树算法应用本节基于 Python Sklearn 机器学习算法库,对决策树这类算法做相关介绍,并对该算法的使用步骤做简单的总结,最后通过应用案例对决策树算法的代码实现进行演示。 决策树算法应用 在 sklearn 库中与决策树相关的算法都存放在 模块里,该模块提供了 4 个决策树算法,下面对这些算法做简单的介绍: 1) .DecisionTreeClassifier() 这是一个经典的决策树分类算法,它提供
-
sklearn实现KNN分类算法
Pyhthon Sklearn 机器学习库提供了 neighbors 模块,该模块下提供了 KNN 算法的常用方法,如下所示: 类方法 说明 KNeighborsClassifier KNN 算法解决分类问题 KNeighborsRegressor KNN 算法解决回归问题 RadiusNeighborsClassifier 基于半径来查找最近邻的分类算法 NearestNeighbors 基于无
-
 KNN最邻近分类算法
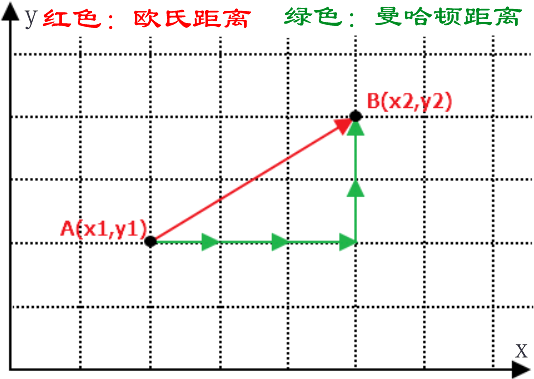
KNN最邻近分类算法主要内容:KNN算法原理,KNN算法流程,KNN预测分类本节继续探机器学习分类算法——K 最近邻分类算法,简称 KNN(K-Nearest-Neighbor),它是有监督学习分类算法的一种。所谓 K 近邻,就是 K 个最近的邻居。比如对一个样本数据进行分类,我们可以用与它最邻近的 K 个样本来表示它,这与俗语“近朱者赤,近墨者黑”是一个道理。 在学习 KNN 算法的过程中,你需要牢记两个关键词,一个是“少数服从多数”,另一个是“距离”,它们是实现 KN
-
 置换选择排序算法
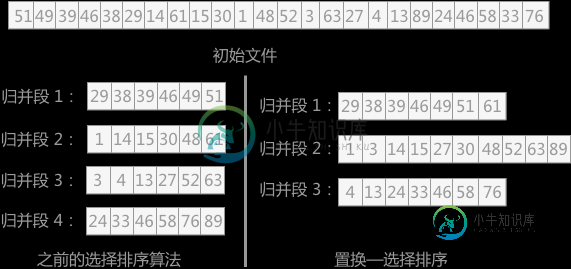
置换选择排序算法主要内容:置换选择排序算法的具体实现,总结上一节介绍了增加 k-路 归并排序中的 k 值来提高外部排序效率的方法,而除此之外,还有另外一条路可走,即减少初始归并段的个数,也就是本章第一节中提到的减小 m 的值。 m 的求值方法为:m=⌈n/l⌉(n 表示为外部文件中的记录数,l 表示初始归并段中包含的记录数) 如果要想减小 m 的值,在外部文件总的记录数 n 值一定的情况下,只能增加每个归并段中所包含的记录数 l。而对于初始归并段的形成,
-
码原序列转换算法
附言。毫无头绪
-
用Java实现模X算法
我正在寻找一种通用模式来分解一些常见的代码:我需要在具有不同算术属性的类之间实现代数加法和减法。一个典型的例子是可以用秒、小时和分钟表示的间隔,我用一个具有三个int属性的类实现了它。 例如,如果我想减去0秒、0分钟、1小时的周期,减去0秒、30分钟、0小时的周期,我不想获得0秒、-30分钟、1小时的周期。 我需要编码两个时间间隔之间的加减法,有没有通用的模式来编码这个代数?我应该寻找不同的代表吗
-
算法问题:字母组合
问题内容: 我正在尝试编写一段代码来执行以下操作: 取数字0到9,并给该数字分配一个或多个字母。例如: 当我有0123这样的代码时,对它进行编码很容易。显然,它将组成代码NLTD。当引入数字5,6或8时,情况会有所不同。051之类的数字可能会导致多种可能性: NVL和NFL 显而易见,较长的数字甚至包括5、6或8这样的数字,甚至会变得“更糟”。 由于对数学非常不好,我还无法提出一个像样的解决方案,
-
javascript - 请教一道算法题?
有以下数据: 要求是,将所有项按顺序一一组合,如 红色8g小米10pro,红色8g小米10plus,红色8g小米11pro,红色8g小米11plus,... 以下是我的暴力解法 再者,不按顺序又该如何解
-
1.8 K 均值聚类算法
$k$均值聚类算法(k-means clustering algorithm) 在聚类的问题中,我们得到了一组训练样本集 ${x^{(1)},...,x^{(m)}}$,然后想要把这些样本划分成若干个相关的“类群(clusters)”。其中的 $x^{(i)}\in R^n$,而并未给出分类标签 $y^{(i)}$ 。所以这就是一个无监督学习的问题了。 $K$ 均值聚类算法如下所示: 随机初始化(
