python实现粒子群算法

粒子群算法

粒子群算法源于复杂适应系统（Complex Adaptive System,CAS）。CAS理论于1994年正式提出，CAS中的成员称为主体。比如研究鸟群系统，每个鸟在这个系统中就称为主体。主体有适应性，它能够与环境及其他的主体进行交流，并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括：新层次的产生（小鸟的出生）；分化和多样性的出现（鸟群中的鸟分成许多小的群）；新的主题的出现（鸟寻找食物过程中，不断发现新的食物）。

PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest,gbest)来更新自己。
在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

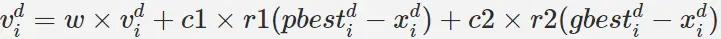
i 表示第 i 个粒子， d 表示粒子的第 d 个维度。r1, r2 表示两个位于 [0, 1] 的随机数（对于一个粒子的不同维度，r1, r2 的值不同）。pbest[i] 是指粒子取得最高（低）适应度时的位置，gbest[i] 指的是整个系统取得最高（低）适应度时的位置。

实践

我们用 PSO 算法求解如下函数的最小值

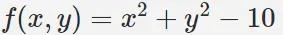
可以在空间画出图像

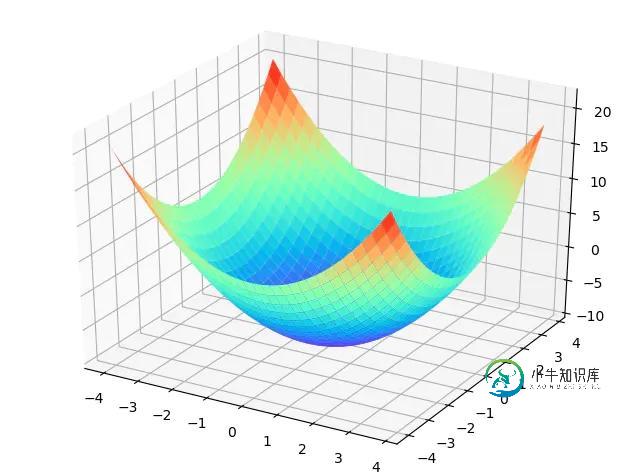
下图是使用 5 个粒子的收敛情况

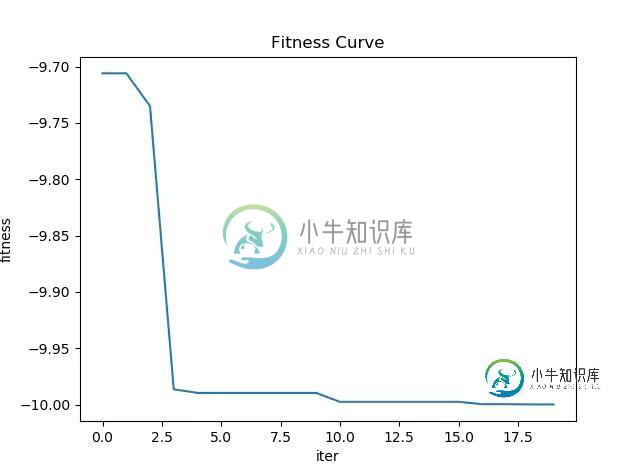
可以看到，fitness 在第 12 轮就几乎收敛到 -10.0。

下面是完整代码

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


INF = 1e5

def plot_cost_func():
  """画出适应度函数"""
  fig = plt.figure()
  ax = Axes3D(fig)
  X = np.arange(-4, 4, 0.25)
  Y = np.arange(-4, 4, 0.25)
  X, Y = np.meshgrid(X, Y)
  Z = (X**2 + Y**2) - 10
  ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
  plt.show()

def fitness(x):
  return x[0]**2 + x[1]**2 - 10

class PSOSolver(object):
  def __init__(self, n_iter, weight=0.5, c1=2, c2=2, n_particle=5):
    self.n_iter = n_iter
    self.weight = weight
    self.c1 = c1
    self.c2 = c2
    self.n_particle = n_particle
    self.gbest = np.random.rand(2)
    # gbest 对应的函数值
    self.gbest_fit = fitness(self.gbest)
    # 将位置初始化到 [-5, 5]
    self.location = 10 * np.random.rand(n_particle, 2) - 5
    # 将速度初始化到 [-1, 1]
    self.velocity = 2 * np.random.rand(n_particle, 2) - 1
    self.pbest_fit = np.tile(INF, n_particle)
    self.pbest = np.zeros((n_particle, 2))
    # 记录每一步的最优值
    self.best_fitness = []
  
  def new_velocity(self, i):
    r = np.random.rand(2, 2)
    v = self.velocity[i]
    x = self.location[i]
    pbest = self.pbest[i]
    return self.weight * v + self.c1 * r[0] * (pbest - x) + \
        self.c2 * r[1] * (self.gbest - x)

  def solve(self):
    for it in range(self.n_iter):
      for i in range(self.n_particle):
        v = self.new_velocity(i)
        x = self.location[i] + v
        fit_i = fitness(x)
        if fit_i < self.pbest_fit[i]:
          self.pbest_fit[i] = fit_i
          self.pbest[i] = x
          if fit_i < self.gbest_fit:
            self.gbest_fit = fit_i
            self.gbest = x
        self.velocity[i] = v
        self.location[i] = x
      self.best_fitness.append(self.gbest_fit)

  
if __name__ == '__main__':
  plot_cost_func()
  n_iter = 20
  s = PSOSolver(n_iter)
  s.solve()
  print(s.gbest_fit)
  plt.title("Fitness Curve")
  plt.xlabel("iter")
  plt.ylabel("fitness")
  plt.plot(np.arange(n_iter), np.array(s.best_fitness))
  plt.show()

以上就是python实现粒子群算法的详细内容，更多关于python 粒子群算法的资料请关注小牛知识库其它相关文章！