略不平衡二叉树中二叉搜索的时间复杂度
如果二叉树是平衡的,那么二叉搜索的最佳运行时间是O(log(n))。最坏的情况是,如果二叉树非常不平衡,它基本上表示一个链表。在这种情况下,二进制搜索的运行时间将为O(n)。
但是,如果树只是稍微不平衡,就像这棵树的情况一样:
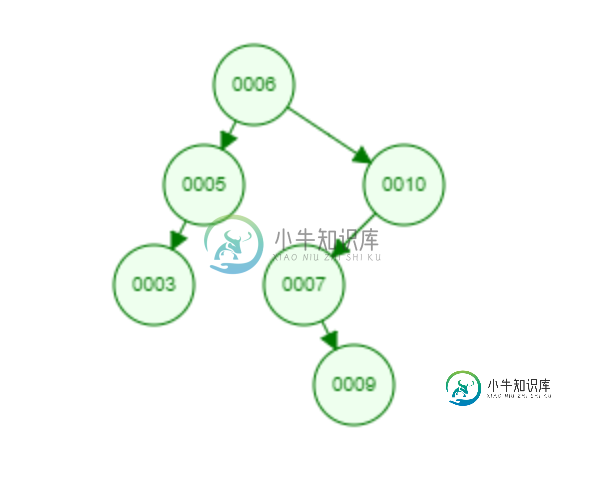
如果我没记错的话,最好的情况仍然是O(log n)。但是最坏的情况是什么?
共有2个答案
通常,当我们说“在平衡二元搜索树中查找元素的成本是O(log n)”时,“我们的意思是“在最坏的情况下,我们必须在平衡二元搜索树上执行搜索的过程中执行O(log n)工作。”由于我们在这里讨论的是big-O符号,所以前面的陈述是关于一般的平衡树,而不是特定的具体树。
如果您考虑了特定的BST,那么可以计算出查找任何元素所需的最大比较次数。只需找到树中最深的节点,然后想象搜索一个大于该值但小于树中下一个值的值。这将使您尽可能深入地沿着树走下去,从而尽可能多地进行比较(特别是其中的h 1,其中h是树的高度)。
为了能够讨论在树中执行查找的大O成本,您需要讨论不同节点数的树族。你可以想象“有点平衡”的树,其深度为(√n) ,例如,查找需要时间(√n) ,例如。然而,在实践中遇到这样的树是很少见的,因为通常情况下,你要么(1)有一棵完全不平衡的树,要么(2)使用某种平衡的树来防止树的高度达到那么高。
在n个值的排序数组中,在最坏的情况下,二进制搜索值的运行时间是O(log n)
在最佳情况下,您正在搜索的元素正好位于中间,并且可以在固定时间内完成
在一般情况下,运行时间也是O(log n)。
-
在上一节中,我们考虑构建一个二叉搜索树。正如我们所学到的,二叉搜索树的性能可以降级到 $$O(n)$$ 的操作,如 get 和 put ,如果树变得不平衡。在本节中,我们将讨论一种特殊类型的二叉搜索树,它自动确保树始终保持平衡。这棵树被称为 AVL树,以其发明人命名:G.M. Adelson-Velskii 和E.M.Landis。 AVL树实现 Map 抽象数据类型就像一个常规的二叉搜索树,唯一
-
在我们继续之前,我们来看看执行这个新的平衡因子要求的结果。我们的主张是,通过确保树总是具有 -1,0或1 的平衡因子,我们可以获得更好的操作性能的关键操作。 让我们开始思考这种平衡条件如何改变最坏情况的树。有两种可能性,一个左重树和一个右重树。 如果我们考虑高度0,1,2和3的树,Figure 2 展示了在新规则下可能的最不平衡的左重树。 Figure 2 看树中节点的总数,我们看到对于高度为0的
-
所以,我一直在研究平衡的二叉查找树。 我谷歌了一下,这是我的发现: 二叉树,其中每个节点的两个子树的深度相差 1 或更小(来自维基百科) 难道就不能把平衡二叉树定义为高度不超过ceil(log(n ^ 1)/log ^ 2)的树吗? 从这个答案来看,提问者似乎已经问了同样的事情,但是公认的答案通过举斐波纳契树的例子拒绝了这个想法。斐波纳契树不是平衡树,对吗?我认为回答者可能会与AVL树中平衡树的定
-
假设BST的高度是h。如果我们要删除一个有两个子节点的节点,那么该过程的时间复杂度是多少。 我知道在普通的二叉树中,删除的时间复杂度是O(h);O(n)最坏情况和O(logn)最好情况。但是由于我们用它的右子树的最小节点替换删除节点的键,因此需要更多时间来找到最小键。 那么,有人知道如何解释这种情况下的时间复杂性吗?
-
我已经知道,如果您尝试查找具有特定键的项目,最坏情况下的运行时间是O(n),。如果您试图搜索特定的数据项(您不知道该键),那么最坏情况下的运行时间是O(n)。然而,如果键和数据都是整数,输入项在插入之前被随机置乱,会怎么样。最糟糕的运行时间还会保持不变吗?
-
如果我有一个平衡的二叉树,并且我想在其中搜索一个项目,那么大的oh时间复杂度会是O(n)吗?在二叉树中搜索一个项目,不管它是否平衡,会改变O(n)的大时间复杂性吗?我知道如果我们有一个平衡的BST,那么搜索一个项目就等于BST的高度so O(log n),但是普通的二叉树呢?

