《二叉树》专题
-
二叉树
二叉树 二叉树采用二叉链表存储,要求根据给定的先序遍历序列和中序遍历序列建立二叉树,并输出后序遍历序列、结点总数、叶子数、度为1的结点数、度为2的结点数。 输入格式: 测试数据有多组,处理到文件尾。每组测试数据的第一行输入结点数n(1≤n≤10),第二、三行各输入n个整数,分别表示二叉树的先序遍历序列和中序遍历序列。 输出格式: 对于每组测试,在一行上分别输出该二叉树的后序遍历序列,结点总数,叶子
-
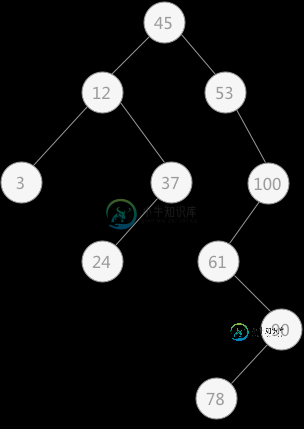 二叉排序树(二叉查找树)
二叉排序树(二叉查找树)主要内容:什么是二叉排序树?,使用二叉排序树查找关键字,二叉排序树中插入关键字,二叉排序树中删除关键字,总结前几节介绍的都是有关静态 查找表的相关知识,从本节开始介绍另外一种查找表—— 动态查找表。 动态查找表中做查找操作时,若查找成功可以对其进行删除;如果查找失败,即表中无该关键字,可以将该关键字插入到表中。 动态查找表的表示方式有多种,本节介绍一种使用树结构表示动态查找表的实现方法—— 二叉排序树(又称为 “二叉查找树”)。 什么是二叉排序树? 二叉排序树要么是空 二叉树,要么具有如下特点:
-
2. 二叉树
2. 二叉树 2.1. 二叉树的基本概念 链表的每个节点可以有一个后继,而二叉树(Binary Tree)的每个节点可以有两个后继。比如这样定义二叉树的节点: typedef struct node *link; struct node { unsigned char item; link l, r; }; 这样的节点可以组织成下图所示的各种形态。 图 26.9. 二叉树的定义和举例 二叉树可
-
二叉树与二叉搜索树Big oh分析
我说得对吗?
-
给定二叉树是否为二叉搜索树
我写了一个函数,如果给定的二叉树是二叉搜索树,则返回true,否则返回false。 我的功能对吗?
-
纸上谈兵: 树, 二叉树, 二叉搜索树
树的特征和定义 树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树: 树有多个节点(node),用以储存元素。某些节点之间存在一定的关系,用连线表示,连线称为边(edge)。边的上端节点称为父节点,下端称为子节点。树像是一个不断分叉的树根。 每个节点可以有多个子节点(children),而该节点是相应子节点的父节点(parent)。比如说,3,5是6的子节点,6是3,
-
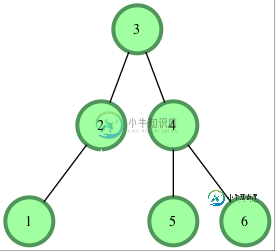 二叉树验证
二叉树验证一直在研究一些黑客等级破解编码面试问题,最近才发现这一个:二叉树问题。 在问题描述中,作者介绍了被认为是有效的二叉树的内容。 “节点左侧子树中每个节点的值都小于该节点的数据值。 然而他们提到这棵树 是有效的。但根据他们对有效二叉搜索树的描述,这棵树不是无效的吗,因为节点4有一个节点5的左子节点,后者更大。还是我误解了什么是有效的BST?
-
二叉查找树
我正在努力实现二叉搜索树。完成实现所需的功能之一是重新平衡功能。 根据规范,该功能的工作方式如下: rebalance() 方法应创建一个平衡树,从而将偏度降低为零。平衡树是指在整个树中,左子树和右子树的大小相差不超过1(即,每个子树也是平衡的)。 为了平衡树,rebalance() 方法应反复将根值移动到较小的子树,并将最小/最大值从较大的子树移动到根,直到树平衡。然后,它应该以递归方式平衡两个
-
线程二叉树
大家好,我应该编写ThreadedNode()类,但是我遇到了一些问题。 我理解,一个二叉树的线程二叉树是通过在顺序遍历中将每一个null左子级设置为节点的前导,在顺序遍历中将每一个null右子级设置为节点的后继来获得的。 但是,我的问题是从构造函数//线程(二叉树)开始的,当您被赋予根公共线程节点(BinaryNode根) 我知道它接收一个binaryNode,我必须使它成为一个线程树,但我如何
-
镜像二叉树
我有一个简单的Node类来构造我的二叉树中的树节点: 我编写了一个简单的Tree类,它将使用节点结构来构建一个树: 如果你能给我指明正确的方向,我将不胜感激。
-
玩转二叉树
玩转二叉树 给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。 输入格式: 输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。 输出格式: 在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分
-
习题7-2 二叉排序树(二叉搜索树)
HLOJ 9576,习题7-2 二叉排序树 输入一个整数关键字序列,生成一棵用链式存储结构存储的二叉排序树,对该二叉排序树能进行查找和插入结点的操作,并对该二叉排序树中结点的关键字按递增和递减顺序输出。 要求依次完成以下工作: (1) 以这n个整数生成(建立)一棵用链式存储结构存储的二叉排序树; (2) 按递增顺序输出该二叉排序树中的整数(关键字); (3) 输入一个整数key1,对该二叉排序树进
-
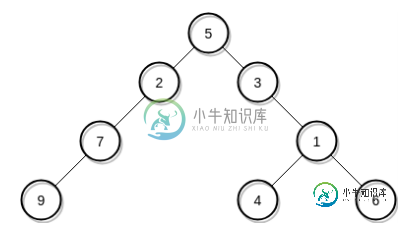 函数将二叉树转换为完整的二叉树?
函数将二叉树转换为完整的二叉树?下面给出了二叉树的实现。 如图中所示,树不是完整的二叉树。如何编写一个函数,将上述二叉树转换为完整的二叉树,只需将字符串数据节点添加到没有子节点的节点,即可生成完整的二叉树。 我将手动在代码中添加节点,以获得如下结果树: 但是,如何编写一个函数,它将采取根节点和返回树,这是完整的二叉树。
-
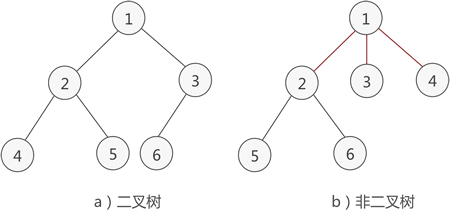 什么是二叉树
什么是二叉树主要内容:二叉树的性质,满二叉树,完全二叉树,总结通过《 树的存储结构》一节的学习,我们了解了一些树存储结构的基本知识。本节将给大家介绍一类具体的树结构—— 二叉树。 简单地理解,满足以下两个条件的树就是二叉树: 本身是有序树; 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2; 例如,图 1a) 就是一棵二叉树,而图 1b) 则不是。 图 1 二叉树示意图 二叉树的性质 经过前人的总结,二叉树具有以下几个性质: 二叉树中,第 i
-
14 二叉树节点
class Node(object): def __init__(self, data, left=None, right=None): self.data = data self.left = left self.right = right tree = Node(1, Node(3, Node(7, Node(0)), Node(6)), Node(2, Node
