函数将二叉树转换为完整的二叉树？

Question

下面给出了二叉树的实现。

class Node:
    def __init__(self, data):
        self.data = data
        self.right = None
        self.left = None


root = Node(5)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(7)
root.left.left.left = Node(9)
root.right.right = Node(1)
root.right.right.right = Node(6)
root.right.right.left = Node(4)

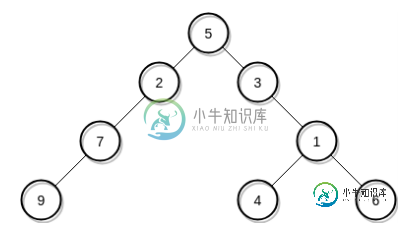
如图中所示，树不是完整的二叉树。如何编写一个函数，将上述二叉树转换为完整的二叉树，只需将字符串数据节点添加到没有子节点的节点，即可生成完整的二叉树。

我将手动在代码中添加节点，以获得如下结果树：

root.left.right = Node('a')
root.right.left = Node('a')
root.right.left.left = Node('a')
root.right.left.right = Node('a')
root.left.right.right = Node('a')
root.left.right.left = Node('a')

但是，如何编写一个函数，它将采取根节点和返回树，这是完整的二叉树。

Answer 1

首先，获取树的高度。这将是完整树的高度。接下来，遍历树，对于每个节点，如果它的深度小于树的高度，并且缺少它的左子节点或右子节点（或两者），则添加缺少的内容，然后继续遍历。因此对于您的输入，该过程将执行

5             h=0
=> 2          h=1
   => 7       h=2
     => 9     h=3
=> 3          h=1
   => 1       h=2
      => 4    h=3
      => 6    h=3

max height seen was 3, so height of tree is 3

5             h < 3, has both children, nothing to add
=> 2          h < 3, missing right child, add 'a'
   => 7       h < 3, missing right child, add 'b'
      => 9    h = 3, nothing to add
      => b    h = 3, nothing to add
   => a       h < 3, missing left and right children, add 'c' and 'd'
      => c    h = 3, nothing to add
      => d    h = 3, nothing to add
=> 3          h < 3, missing left child, add 'e'
   => e       h < 3, missing left and right children, add 'f' and 'g'
      => f    h = 3, nothing to add
      => g    h = 3, nothing to add
   => 1       h < 3, has both children, nothing to add
      => 4    h = 3, nothing to add
      => 6    h = 3, nothing to add

我们看到，这添加了与手动相同的节点（实际上可能遗漏了一个，7在图形中只有一个子节点）。我们将它们标记为a、b、c、d、e、f和g，但您可以编写代码，这样它就可以为它们提供相同的字符串。

Answer 2

您将需要创建一个可以为您提供树中最大深度的方法。从中，您可以添加一个方法来递归地将空节点添加到该深度：

class Node:
    def __init__(self, data):
        self.data = data
        self.right = None
        self.left = None

    @property
    def maxDepth(self): # compute maximum depth (i.e. levels under self)
        depth = 0
        if self.left:  depth = self.left.maxDepth+1
        if self.right: depth = max(depth,self.right.maxDepth+1)
        return depth

    def expandToDepth(self,depth=None): # add empty nodes to fill tree
        if depth is None: depth = self.maxDepth
        if not depth: return
        if not self.left:  self.left  = Node(None)
        if not self.right: self.right = Node(None)
        self.left.expandToDepth(depth-1)
        self.right.expandToDepth(depth-1)

    def __repr__(self): # this is just to print the tree
        nodeInfo = lambda n: (str(n.data or "?"),n.left,n.right)
        return "\n".join(printBTree(self,nodeInfo,isTop=False))

输出：

root = Node(5)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(7)
root.left.left.left = Node(9)
root.right.right = Node(1)
root.right.right.right = Node(6)
root.right.right.left = Node(4)

## BEFORE ##
print(root)

      5
     / \
    2   3
   /     \
  7       1
 /       / \
9       4   6

root.expandToDepth()

## AFTER ##
print(root)

             5
       _____/ \_____
      2             3
   __/ \_        __/ \_
  7      ?      ?      1
 / \    / \    / \    / \
9   ?  ?   ?  ?   ?  4   6

printBTree（）是我提供的一个函数，用于回答另一个问题：https://stackoverflow.com/a/49844237/5237560

这是它的副本（以防链接消失）：

import functools as fn

def printBTree(node, nodeInfo=None, inverted=False, isTop=True):

       # node value string and sub nodes
       stringValue, leftNode, rightNode = nodeInfo(node)

       stringValueWidth  = len(stringValue)

       # recurse to sub nodes to obtain line blocks on left and right
       leftTextBlock     = [] if not leftNode else printBTree(leftNode,nodeInfo,inverted,False)

       rightTextBlock    = [] if not rightNode else printBTree(rightNode,nodeInfo,inverted,False)

       # count common and maximum number of sub node lines
       commonLines       = min(len(leftTextBlock),len(rightTextBlock))
       subLevelLines     = max(len(rightTextBlock),len(leftTextBlock))

       # extend lines on shallower side to get same number of lines on both sides
       leftSubLines      = leftTextBlock  + [""] *  (subLevelLines - len(leftTextBlock))
       rightSubLines     = rightTextBlock + [""] *  (subLevelLines - len(rightTextBlock))

       # compute location of value or link bar for all left and right sub nodes
       #   * left node's value ends at line's width
       #   * right node's value starts after initial spaces
       leftLineWidths    = [ len(line) for line in leftSubLines  ]                            
       rightLineIndents  = [ len(line)-len(line.lstrip(" ")) for line in rightSubLines ]

       # top line value locations, will be used to determine position of current node & link bars
       firstLeftWidth    = (leftLineWidths   + [0])[0]  
       firstRightIndent  = (rightLineIndents + [0])[0] 

       # width of sub node link under node value (i.e. with slashes if any)
       # aims to center link bars under the value if value is wide enough
       # 
       # ValueLine:    v     vv    vvvvvv   vvvvv
       # LinkLine:    / \   /  \    /  \     / \ 
       #
       linkSpacing       = min(stringValueWidth, 2 - stringValueWidth % 2)
       leftLinkBar       = 1 if leftNode  else 0
       rightLinkBar      = 1 if rightNode else 0
       minLinkWidth      = leftLinkBar + linkSpacing + rightLinkBar
       valueOffset       = (stringValueWidth - linkSpacing) // 2

       # find optimal position for right side top node
       #   * must allow room for link bars above and between left and right top nodes
       #   * must not overlap lower level nodes on any given line (allow gap of minSpacing)
       #   * can be offset to the left if lower subNodes of right node 
       #     have no overlap with subNodes of left node                                                                                                                                 
       minSpacing        = 2
       rightNodePosition = fn.reduce(lambda r,i: max(r,i[0] + minSpacing + firstRightIndent - i[1]), \
                                     zip(leftLineWidths,rightLineIndents[0:commonLines]), \
                                     firstLeftWidth + minLinkWidth)

       # extend basic link bars (slashes) with underlines to reach left and right
       # top nodes.  
       #
       #        vvvvv
       #       __/ \__
       #      L       R
       #
       linkExtraWidth    = max(0, rightNodePosition - firstLeftWidth - minLinkWidth )
       rightLinkExtra    = linkExtraWidth // 2
       leftLinkExtra     = linkExtraWidth - rightLinkExtra

       # build value line taking into account left indent and link bar extension (on left side)
       valueIndent       = max(0, firstLeftWidth + leftLinkExtra + leftLinkBar - valueOffset)
       valueLine         = " " * max(0,valueIndent) + stringValue
       slash             = "\\" if inverted else  "/"
       backslash         = "/" if inverted else  "\\"
       uLine             = "¯" if inverted else  "_"

       # build left side of link line
       leftLink          = "" if not leftNode else ( " " * firstLeftWidth + uLine * leftLinkExtra + slash)

       # build right side of link line (includes blank spaces under top node value) 
       rightLinkOffset   = linkSpacing + valueOffset * (1 - leftLinkBar)                      
       rightLink         = "" if not rightNode else ( " " * rightLinkOffset + backslash + uLine * rightLinkExtra )

       # full link line (will be empty if there are no sub nodes)                                                                                                    
       linkLine          = leftLink + rightLink

       # will need to offset left side lines if right side sub nodes extend beyond left margin
       # can happen if left subtree is shorter (in height) than right side subtree                                                
       leftIndentWidth   = max(0,firstRightIndent - rightNodePosition) 
       leftIndent        = " " * leftIndentWidth
       indentedLeftLines = [ (leftIndent if line else "") + line for line in leftSubLines ]

       # compute distance between left and right sublines based on their value position
       # can be negative if leading spaces need to be removed from right side
       mergeOffsets      = [ len(line) for line in indentedLeftLines ]
       mergeOffsets      = [ leftIndentWidth + rightNodePosition - firstRightIndent - w for w in mergeOffsets ]
       mergeOffsets      = [ p if rightSubLines[i] else 0 for i,p in enumerate(mergeOffsets) ]

       # combine left and right lines using computed offsets
       #   * indented left sub lines
       #   * spaces between left and right lines
       #   * right sub line with extra leading blanks removed.
       mergedSubLines    = zip(range(len(mergeOffsets)), mergeOffsets, indentedLeftLines)
       mergedSubLines    = [ (i,p,line + (" " * max(0,p)) )       for i,p,line in mergedSubLines ]
       mergedSubLines    = [ line + rightSubLines[i][max(0,-p):]  for i,p,line in mergedSubLines ]                        

       # Assemble final result combining
       #  * node value string
       #  * link line (if any)
       #  * merged lines from left and right sub trees (if any)
       treeLines = [leftIndent + valueLine] + ( [] if not linkLine else [leftIndent + linkLine] ) + mergedSubLines

       # invert final result if requested
       treeLines = reversed(treeLines) if inverted and isTop else treeLines

       # return intermediate tree lines or print final result
       if isTop : print("\n".join(treeLines))
       else     : return treeLines