javascript实现二叉树的代码

前言：

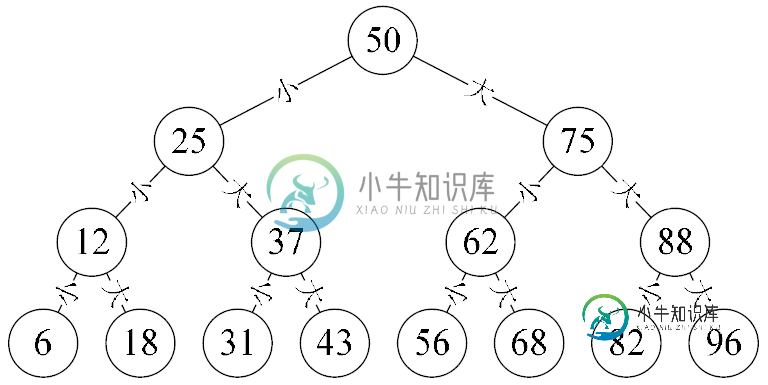
二叉树的特点(例图只是二叉树的一种情况，不要尝试用例图推理以下结论)

1. 除了最下面一层，每个节点都是父节点，每个节点都有且最多有两个子节点；
2. 除了嘴上面一层，每个节点是子节点，每个节点都会有一个父节点；
3. 最上面一层的节点（即例图中的节点50）为根节点；

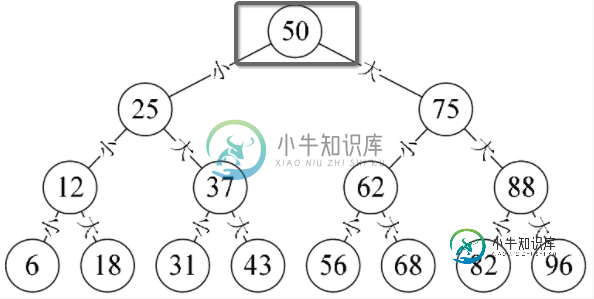
最下面一层的节点称为叶子节点，他们没有子节点；

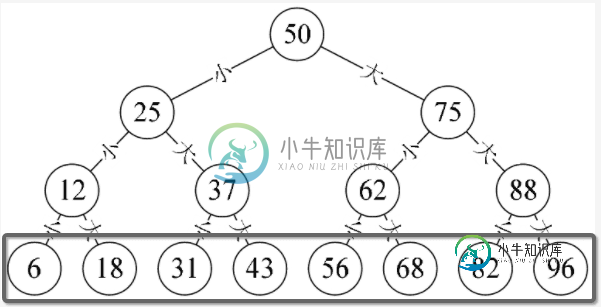
左子节点的值 < 父节点的值 <= 右节点的值

1 节点的javascript实现

// 节点对象
function Node(data, left, right) {
  this.data = data; // 节点值
  this.left = left; // 当前节点的左子节点
  this.right = right; // 当前节点的右子节点
  this.show = show; // 辅助function
}

function show() {
  return this.data;
}

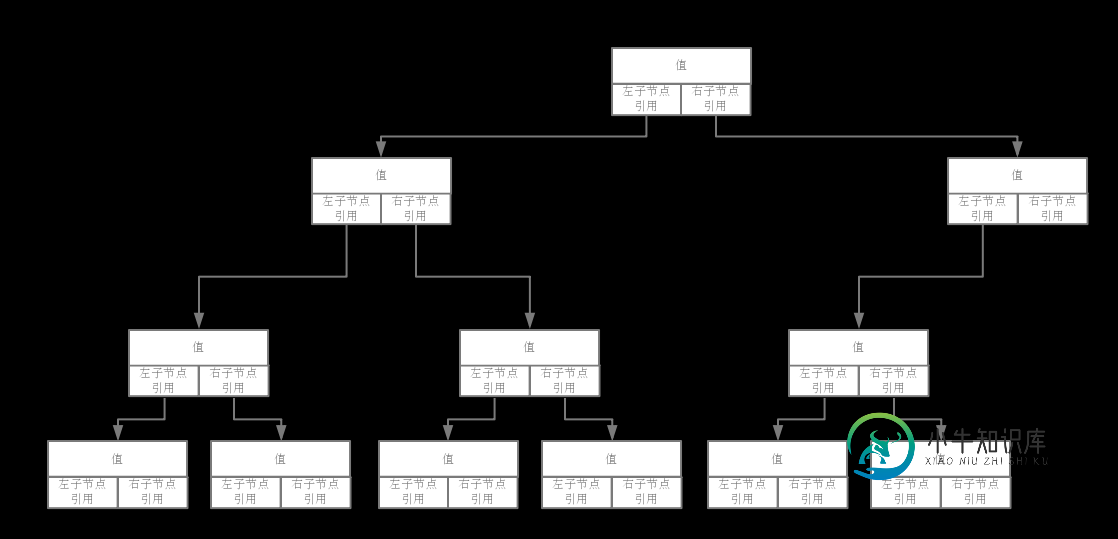
感受下上面实现节点的代码，感觉和链表有点相似不是吗，存着当前值，又存着下个节点（左、右子节点）的引用，下面是一张伪代码的草图：

2 二叉树的实现

实现二叉树，当然就是要插入节点构成二叉树，先看看实现二叉树的js代码

function BST() {
  this.root = null;
  this.insert = insert;
}

function insert(data) {
  var n = new Node(data, null, null);
  if (this.root == null) {
   this.root = n;
  }
  else {
   var current = this.root;
   var parent;
   while (true) {
     parent = current;
     if (data < current.data) {
      current = current.left;
      if (current == null) {
        parent.left = n;
        break;
      }
     }
     else {
      current = current.right;
      if (current == null) {
        parent.right = n;
        break;
      }
     }
   }
  }
}

然后是看一下伪代码：

function BST() {
  this.root = null; // 根节点
  this.insert = insert;
}

function insert(data) {
  // 初始化一个节点，为什么要将左右子节点的引用初始化为空呢，因为可能是叶子节点，加入他有子节点，会在下面的代码添加
  var n = new Node(data, null, null);
  if (该二叉树是否为空，是空则根节点为空，因此可以用根节点判断二叉树是否为空) {
   // 将当前节点存为根节点
   this.root = n;
  }
  else {
   // 来到这里就表示，该二叉树不为空，这里关键的是两句代码：
   // 0.while (true);
   // 1.parent = current；
   // 2.current = current.left;/current = current.right;
   // 3.break;
   var current = this.root;
   var parent;
   while (true) {
     parent = current; // 获得父节点，第一次循环，那么父节点就是根节点
     if (data < current.data) { // 当前节点值小于父节点的值就是存左边，记得二叉树的特点吧，如果真是小于父节点，那么就说明该节点属于，该父节点的左子树。
      current = current.left;
      if (current == null) {
        parent.left = n;
        break;
      }

      // 其实上面这样写不好理解，可以等价于下面的代码：
      // start
      if(current.left == null){ // 若果左节点空，那么这个空的节点就是我们要插入的位置
        current.left = n;
        break;
      }else{
        // 不空则继续往下一层找空节点（插入的位置）
        current = current.left;
      }
      // end
     }
     else {
      // 右节点的逻辑代码个左节点的一样的
      current = current.right;
      if (current == null) {
        parent.right = n;
        break;
      }
     }
   }
  }
}

下面是一个更好理解的插入函数

function insert(data) {
  var n = new Node(data, null, null);
  if (this.root == null) {
   this.root = n;
  }
  else {
   var current = this.root;
   // start change
   while (true) {
     if (data < current.data) {
      if (current.left == null) {
        current.left = n;
        break;
      }else{
        current = current.left;
      }
     }else {
      if (current.right == null) {
        current.right = n;
        break;
      }else{
        current = current.right;
      }
     }
   }
  }
}

小结：

二叉树的实现的三个部件

Node对象

function Node(data, left, right) { ... }

BST对象

function BST() { ... }

插入节点函数

function insert(data) { ... }

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。