JAVA 实现二叉树（链式存储结构）

二叉树的分类（按存储结构）

树的分类（按存储结构）

             　顺序存储（用数组表示（静态二叉树））
　　　　  链式存储

一些特别的二叉根：

                                   完全二叉树，平衡二叉树（AVL），线索二叉树，三叉的（带父亲的指针）
　　　　　　　　　   二叉搜索树或者叫二叉　查找树（BST）

 所用二叉树如下图所示：

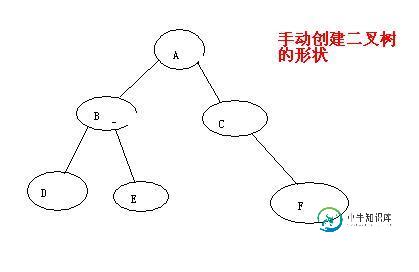
二叉树的Java实现（链式存储结构）

class TreeNode {
  private int key = 0;
  private String data = null;
  private boolean isVisted = false;
  private TreeNode leftChild = null;
  private TreeNode rightChild = null;
  
  public TreeNode(){
    
  }
  public TreeNode(int key, String data){
    this.key = key;
    this.data = data;
    this.leftChild = null;
    this.rightChild = null;
  }
  public int getKey() {
    return key;
  }
  public void setKey(int key) {
    this.key = key;
  }
  public String getData() {
    return data;
  }
  public void setData(String data) {
    this.data = data;
  }
  public TreeNode getLeftChild() {
    return leftChild;
  }
  public void setLeftChild(TreeNode leftChild) {
    this.leftChild = leftChild;
  }
  public TreeNode getRightChild() {
    return rightChild;
  }
  public void setRightChild(TreeNode rightChild) {
    this.rightChild = rightChild;
  }
  public boolean isVisted() {
    return isVisted;
  }
  public void setVisted(boolean isVisted) {
    this.isVisted = isVisted;
  }
}

public class BinaryTree {

  private TreeNode root = null;

  public BinaryTree() {
    root = new TreeNode(1, "rootNode(A)");
  }
  public void createBinTree(TreeNode root){
    //手动的创建（结构如图所示）
    TreeNode newNodeB = new TreeNode(2,"B");
    TreeNode newNodeC = new TreeNode(3,"C");
    TreeNode newNodeD = new TreeNode(4,"D");
    TreeNode newNodeE = new TreeNode(5,"E");
    TreeNode newNodeF = new TreeNode(6,"F");
    root.setLeftChild(newNodeB);
    root.setRightChild(newNodeC);
    root.getLeftChild().setLeftChild(newNodeD);
    root.getLeftChild().setRightChild(newNodeE);
    root.getRightChild().setRightChild(newNodeF);
  }
  public boolean IsEmpty() {
    // 判二叉树空否
    return root == null;
  }

  public int Height() {
    // 求树高度
    return Height(root);
  }

  public int Height(TreeNode subTree) {
    if (subTree == null)
      return 0; //递归结束：空树高度为0
    else {
      int i = Height(subTree.getLeftChild());
      int j = Height(subTree.getRightChild());
      return (i < j) ? j + 1 : i + 1;
    }

  }

  public int Size() {
    // 求结点数
    return Size(root);
  }

  public int Size(TreeNode subTree) {
    if (subTree == null)
      return 0;
    else {
      return 1 + Size(subTree.getLeftChild())
          + Size(subTree.getRightChild());
    }
  }

  public TreeNode Parent(TreeNode element) {
    //返回双亲结点
    return (root == null || root == element) ? null : Parent(root, element);
  }

  public TreeNode Parent(TreeNode subTree, TreeNode element) {

    if (subTree == null)
      return null;
    if (subTree.getLeftChild() == element
        || subTree.getRightChild() == element)
      //找到, 返回父结点地址
      return subTree;
    TreeNode p;
    //先在左子树中找，如果左子树中没有找到，才到右子树去找
    if ((p = Parent(subTree.getLeftChild(), element)) != null)
      //递归在左子树中搜索
      return p;
    else
      //递归在左子树中搜索
      return Parent(subTree.getRightChild(), element);

  }

  public TreeNode LeftChild(TreeNode element) {
    //返回左子树
    return (element != null) ? element.getLeftChild() : null;
  }

  public TreeNode RightChild(TreeNode element) {
    //返回右子树
    return (element != null) ? element.getRightChild() : null;
  }

  public TreeNode getRoot() {
    //取得根结点
    return root;
  }

  public void destroy(TreeNode subTree) {
    //私有函数: 删除根为subTree的子树
    if (subTree != null) {
      destroy(subTree.getLeftChild()); //删除左子树
      destroy(subTree.getRightChild()); //删除右子树
      //delete subTree;       //删除根结点
      subTree = null;
    }
  }

  public void Traverse(TreeNode subTree) {

    System.out.println("key:" + subTree.getKey() + "--name:"
        + subTree.getData());
    Traverse(subTree.getLeftChild());
    Traverse(subTree.getRightChild());
  }

  public void PreOrder(TreeNode subTree) {
    //先根
    if (subTree != null) {
      visted(subTree);
      PreOrder(subTree.getLeftChild());
      PreOrder(subTree.getRightChild());
    }
  }

  public void InOrder(TreeNode subTree) {
    //中根
    if (subTree != null) {
      InOrder(subTree.getLeftChild());
      visted(subTree);
      InOrder(subTree.getRightChild());
    }
  }

  public void PostOrder(TreeNode subTree) {
    //后根
    if (subTree != null) {
      PostOrder(subTree.getLeftChild());
      PostOrder(subTree.getRightChild());
      visted(subTree);
    }
  }
  public void LevelOrder(TreeNode subTree) {
     //水平遍边
  }
  public boolean Insert(TreeNode element){
    //插入
    return true;
  }
  public boolean Find(TreeNode element){
    //查找
    return true;
  }
  public void visted(TreeNode subTree) {
    subTree.setVisted(true);
    System.out.println("key:" + subTree.getKey() + "--name:"
        + subTree.getData());
  }

  public static void main(String[] args) {
    BinaryTree bt = new BinaryTree();
    bt.createBinTree(bt.root);
    System.out.println("the size of the tree is " + bt.Size());
    System.out.println("the height of the tree is " + bt.Height());
    System.out.println("*******先根(前序)[ABDECF]遍历*****************");
    bt.PreOrder(bt.root);
    System.out.println("*******中根(中序)[DBEACF]遍历*****************");
    bt.InOrder(bt.root);
    System.out.println("*******后根(后序)[DEBFCA]遍历*****************");
    bt.PostOrder(bt.root);
  }

}

 结果输出：
the size of the tree is 6
the height of the tree is 3
*******先根(前序)[ABDECF]遍历*****************
key:1--name:rootNode(A)
key:2--name:B
key:4--name:D
key:5--name:E
key:3--name:C
key:6--name:F
*******中根(中序)[DBEACF]遍历*****************
key:4--name:D
key:2--name:B
key:5--name:E
key:1--name:rootNode(A)
key:3--name:C
key:6--name:F
*******后根(后序)[DEBFCA]遍历*****************
key:4--name:D
key:5--name:E
key:2--name:B
key:6--name:F
key:3--name:C
key:1--name:rootNode(A)

 希望本文对学习JAVA程序设计的同学有所帮助。