等效二叉树练习，实现"并发"

Question

我正在解围棋中的练习，等价的二叉树。此练习需要实现一个Walk函数，该函数将遍历一棵树，并将所有值有序地从树发送到通道。

演习声明指出：

...我们将使用Go的并发和通道编写一个简单的解决方案。

阅读这一行，我认为实现Walk是一个挑战，它为每个左/右子树启动一个goroutine，并使Walk比非并发版本运行得更快（关于时间复杂度）。让我用代码更详细地解释一下。

这是我早期的行走代码：

func Walk(t *tree.Tree, ch chan int) {
    defer close(ch)
    if t == nil { return }
    
    lch, rch := make(chan int), make(chan int)
    go Walk(t.Left, lch)
    for v := range lch { ch <- v }

    ch <- t.Value

    go Walk(t.Right, rch)
    for v := range rch { ch <- v }

    return
}

它当然使用goroutines，但实际上与没有goroutines的遍历没有什么不同，因为v：=range lch{...}延迟go Walker（t.右，rch）直到它结束。

向上移动没有任何区别go Walker（t.右，rch）：

func Walk(t *tree.Tree, ch chan int) {
    defer close(ch)
    if t == nil { return }
    
    lch, rch := make(chan int), make(chan int)
    go Walk(t.Left, lch)
    go Walk(t.Right, rch)

    for v := range lch { ch <- v }
    ch <- t.Value
    for v := range rch { ch <- v }
}

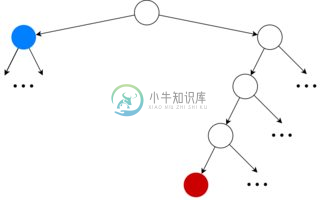
走（t.左，lch）沿着整个左子树（以蓝色为根）行走，并且立即接收从lch发送的值。

走（t.右，rch）试图走，但被阻止作为ch

我的问题是：如何实现Walk，使goroutines（对应于左或右）避免被ch阻塞




Answer 1

右子树中的值需要一个缓冲区（例如缓冲通道），因为它们必须持续到这些值之前（

为大小未知的子树准备缓冲区有几个含义

• 如果使用了缓冲通道，make（chan int，N），则选择N至关重要。如果N恰好对于子树来说太小，则子树的goroutine会很快阻塞。如果内存太大，则会不必要地浪费内存

在我看来，这类问题没有简单而通用的解决方案，“遍历一个随机的、未知的树，并发被挤出”。