雨水收集的时间复杂性

Question

从方法1开始，我一直在研究Leetcode问题的不同算法。如果阵列值是墙的高度，则需要计算总水域面积（列宽=1）。

第一种方法是找出每根立柱左右两侧最大墙高的最小高度，如果立柱高度小于最小值，则向给定立柱顶部加水。取最小值，因为这是收集的水能够达到的最高值。要计算每侧的最大值，需要对左侧和右侧进行n-1次遍历。

我用Python编写代码，但下面是根据Leetcode上给出的解决方案用C编写的代码。问题不在于理解C，而在于理解代码后解释的数学。

int trap(vector<int>& height)
{
    int ans = 0;
    int size = height.size();
    for (int i = 1; i < size - 1; i++) {
        int max_left = 0, max_right = 0;
        for (int j = i; j >= 0; j--) { //Search the left part for max bar size
            max_left = max(max_left, height[j]);
        }
        for (int j = i; j < size; j++) { //Search the right part for max bar size
            max_right = max(max_right, height[j]);
        }
        ans += min(max_left, max_right) - height[i];
    }
    return ans;
}

我不明白的是它们是如何达到时间复杂性O（n^2）的。我得到了O（n^3）。

Index | Comparisons/Traversals
-------------------------------
  1   |            n
  2   |            n
  3   |            n
  4   |            n
  .   |            .
  .   |            .
  .   |            .
 n-1  |            n

此处执行的总操作数为：n 2n 3n 4n n（n-1）n^2

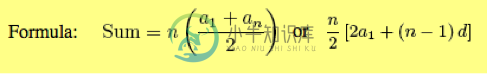
上面的总和最终将是：

Sum = n * [n + n(n-1)]/ 2 = n * [n + n^2- n)]/ 2 = (n^3)/2

这将给出O（n^3）。

我的推理错了什么？它似乎是O（n^2），因为GeeksForGeeks也指出了这一点。

Answer 1

该算法的复杂性也可以通过考虑您有2个嵌套循环这一事实来更容易地看出。所有内部操作都是O（1），因此无论如何它们都不会增加复杂性。考虑嵌套循环，很明显该算法是有序的O（n^2），因为循环的范围是n并且步骤是1。

Answer 2

问题在于：

此处执行的总操作数为：n 2n 3n 4n n（n-1）n^2

但是表的每一行只是n，而不是n，2n，...， n^2。

快速浏览一下，很明显你也正确地填写了表格：内部循环有O（n）恒定的时间步长。

您正在做的所有其余数学都是正确的，但无关紧要。要总结n的n副本，您只需多个n*n，这当然是n^2，而不是O（n^3）。