时间复杂性澄清
给定一个非空字符串s和一个包含非空单词列表的字典字词,确定s是否可以被分割成一个或多个字典单词的空格分隔序列。您可以假定字典不包含重复的单词。
例如,给定s=“leetcode”,dict=[“leet”,“code”]。
返回true,因为“leetcode”可以分段为“leetcode”。
朴素解给出如下:
public class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
return word_Break(s, new HashSet(wordDict), 0);
}
public boolean word_Break(String s, Set<String> wordDict, int start) {
if (start == s.length()) {
return true;
}
for (int end = start + 1; end <= s.length(); end++) {
if (wordDict.contains(s.substring(start, end)) && word_Break(s, wordDict, end)) {
return true;
}
}
return false;
}
}
时间复杂度被列为O(n^n),因为这是递归树的大小。我完全同意递归树的最后一层有n^n个元素,但在该层之前的不是有n^(N-1)吗?所以我们看的是n^n+n^(N-1)+n^(N-2)...导致更高的时间复杂度,对吗?
共有1个答案
让我们从时间复杂度函数的上界的一个简单递推关系开始(即假设它循环整个过程而没有找到匹配):
这里i是start,而n是s.length()。每个术语对应于:
>
word_break,使用start=end,其中end是j第二:调用worddict.contains,子字符串长度end-start+1。
因为Worddict是一个哈希集,所以这个调用是O(L),其中L是输入单词的长度(因为我们需要复制子字符串并对其进行哈希)
扩展的:
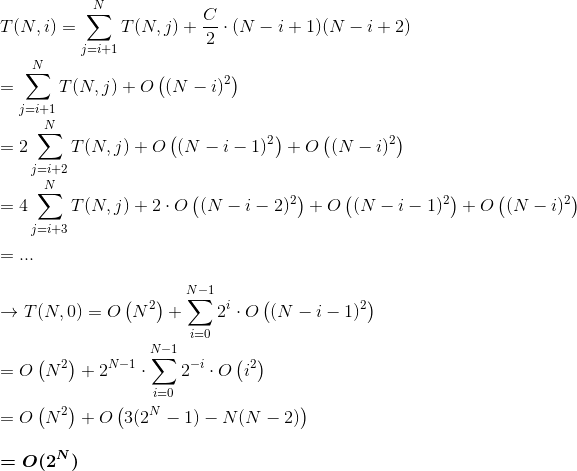
(Wolfram alpha的最后一步)
uint64_t T(uint32_t N, uint32_t start)
{
if (start >= N) return 1;
uint64_t sum = 0;
for (uint32_t end = start + 1; end <= N; end++)
sum += (end - start + 1) + T(N, end);
return sum;
}
N T(N)
-----------------
1 3
2 9
3 22
4 49
5 104
6 215
7 438
8 885
9 1780
10 3571
11 7154
12 14321
13 28656
14 57327
15 114670
16 229357
17 458732
18 917483
19 1834986
20 3669993
21 7340008
22 14680039
23 29360102
24 58720229
25 117440484
26 234880995
27 469762018
28 939524065
29 1879048160
30 3758096351
31 7516192734
32 15032385501
33 30064771036
34 60129542107
时间复杂度的对数标度图:
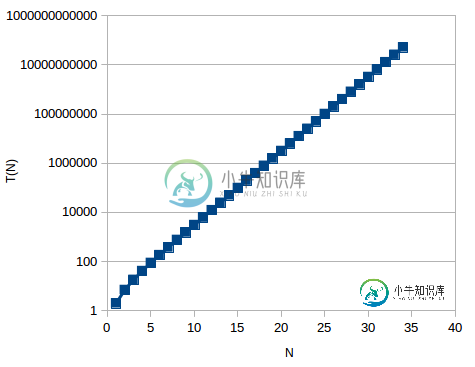
正如您所看到的,这是线性的,这意味着时间复杂度的形式为a^n,而不是n^n。
相比之下,t(N)=O(N^N)将给出如下图:
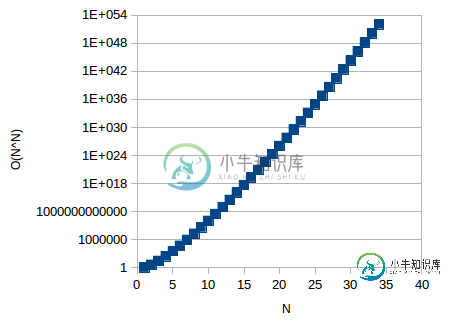
-
我一直在尝试Codility.com的编码挑战,这是我尝试的问题之一: 给出一个由 N 个整数组成的非空零索引数组 A。一对整数 (P, Q),使得 0 ≤ P 例如,数组A如下: 包含以下示例切片: 切片 (1, 2),其平均值为 (2 2) / 2 = 2;切片 (3, 4),其平均值为 (5 1) / 2 = 3;切片 (1, 4),其平均值为 (2 2 5 1) / 4 = 2.5。目标是
-
有一个与数组相关的问题,要求是时间复杂度为O(n),空间复杂度为O(1)。 如果我使用< code>Arrays.sort(arr),并使用< code>for循环进行一次循环,例如: } 所以循环将花费O(n)时间。我的问题是:< code>Arrays.sort()会花费更多时间吗?如果我使用< code>Arrays.sort(),这个时间复杂度还是O(n)吗?< code>Arrays.s
-
我找不到关于它的任何信息,所以我希望你能帮助我。问题是关于for循环中嵌套的else-ifs和时间复杂度计算。 我拥有的一般代码是: 若为O(1),则每个(___)都是复杂度。我遇到的问题是,由于else和嵌套的if-else,我一直对如何计算非简化的big-O复杂度感到困惑。是O(n*1 1 1 1)吗?或者可能是O(n*1 1*(1 1))?我该怎么做呢?
-
主要内容:时间复杂度,空间复杂度《 算法是什么》一节提到,解决一个问题的算法可能有多种,这种情况下,我们就必须对这些算法进行取舍,从中挑选出一个“最好”的。 算法本身是不分“好坏”的,所谓“最好”的算法,指的是最适合当前场景的算法。挑选算法时,主要考虑以下两方面因素: 执行效率:根据算法所编写的程序,执行时间越短,执行效率就越高; 占用的内存空间:不同算法编写出的程序,运行时占用的内存空间也不相同。如果实际场景中仅能使用少量的内
-
这段代码的时间复杂度是多少?外循环运行n次,但我不确定内循环。如果内环对于i的每个值一直运行到n,它能是O(n^2)吗?

