一种将一定大小的矩形放入矩阵自由区域的算法
问题
我需要将大小为n×m的矩形放置在大小为n×m的矩阵的自由区域中,其中n=n*2-1,m=m*2-1。如果矩阵单元为true,则认为它是自由的;如果矩阵单元为false,则认为它是被占用的。由于矩形和矩阵的大小,中心单元格始终为true,并且始终位于矩形内。
附加要求是矩形左上角和中心单元格之间的距离必须尽可能小。
n=8和m=5的示例:
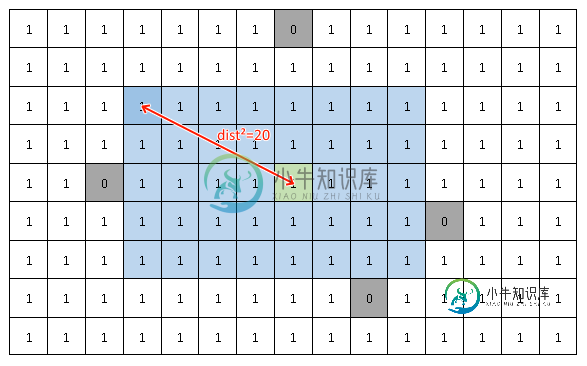
其中灰色单元格-占位,绿色-中心单元格,蓝色单元格-解矩形,红线-矩形左上角和中心单元格之间的距离。
尝试蛮力解的时间复杂度为O(N×M×N×M),这不是非常最优的。若我对矩阵进行预处理,我可以消除某些单元格中的计算,但这仍然需要太多时间。
起初,我认为我可以解决最大矩形问题,只需将条件从最大值修改为所需,但它走到了尽头(我需要在直方图中列出所有矩形,我不知道如何)。然后我认为这就像是包装问题,但我能找到的只是它的版本,最初是完全空的空间和多个矩形,这不适用于这个问题。
过去,当用户单击网格时,如果矩形是空的,我的程序会放置矩形,左上角与单击点重合,如果它占据了矩形放置的单元格,则会失败。我决定修改这个行为,并没有失败,而是为矩形找到最合适的位置,同时仍然包含一个点击点。在上面的矩阵图中,点击点是一个绿色单元格,矩阵大小表示矩形的所有可能位置。
P、 如果可能的话,我更喜欢真实的语言示例而不是伪代码。我的程序是用Java编写的,但任何语言都可以。
共有1个答案
匿名用户
您可以通过以下方式在空间和时间复杂性中执行此操作:
- 计算O(N.M)中的总面积表
- 迭代所有左上角,检查矩形中的总面积是否等于n.m,如果到中心的距离有所改善,则更新最佳位置。每个左上角的测试是O(1),并且左上角有O(N.M),因此总体上是O(N.M)
关键思想是求和面积表允许您在O(1)时间内计算任意矩形的总和。
-
我有一个点[xmin,ymin,xmax,ymax]的列表,每个点都按黑点显示 请注意,有许多这样的矩形,如图像所示。红色的应检测删除,绿色的应保留。 输入是 n 矩形 输出是覆盖区域和它覆盖的矩形 id 。最好给出一些算法和解释。
-
假设我有一组矩形(维度不同或相同)。 任务是从集合中查找(并删除)大于或等于给定矩形的矩形 它也应该是集合中可以包含给定矩形的最小矩形 这很容易通过线性搜索/更新在O(n)时间内解决,但是有可能获得更好的结果吗?我认为O(log n)是最佳值。Insert和removal也必须比O(n)快,这样在我的例子中才有用。 是否可以通过不找到最佳矩形来制定任何快捷方式,而是将第二个限制放宽为:“它也应该是
-
我正在as3中编写一个冲突检测系统。它的目的很简单:我有一些移动的矩形和一些静态的矩形。当一个移动的矩形与另一个矩形碰撞时,我想将源(碰撞)矩形移动到碰撞区域之外,但仍然尽可能靠近(基于源的轨迹)。 在每一帧中,我更新移动矩形的位置,并检查所有矩形之间的接触。 下图代表以下内容: A:方框#1正以45度角向静态矩形(#2)移动。 b:经过几次“刻度”后,我们看到矩形#1移动到矩形#2(静态)的空间
-
我用直方图解决方案编写了这段代码,但用户将输入其矩阵,而不是在代码上输入矩阵。现在看看我做错了什么,除了柱状图的数学之外,一切似乎都正常。我做错了什么? 用户将输入行和列,然后一个接一个地输入矩阵中的每个值。然后代码将显示矩阵并计算所有1的最大大小矩形二进制子矩阵。
-
问题内容: 我正在尝试编写一种算法,用于在给定的子矩阵中查找子矩阵。为了解决这个问题,我编写了以下代码: 这段代码可以正常工作,但是我不确定这是问题的确切解决方案还是可以解决。请提供您的专家意见。提前致谢。 问题答案: 该算法对4×4矩阵和2×2子矩阵进行了硬编码。否则,它看起来像蛮力算法。 我会这样表示: 如果您想要更有效的方法,建议您将它们压扁,如下所示: 并在此序列中搜索以下模式: 使用标准
-
在上面的图片中,我展示了两个矩形 矩形1,其x可以从-900到13700不等,Y可以从-600到6458 矩形2,其坐标X可以从0到3000变化,而y可以从0到2000变化 同样:矩形2的起点位于左上角位置(0,0),而矩形1的起点位于左上角位置(宽度/2,高度/2)。 我需要做的是:使用缩放或平移将矩形1的点转换为矩形2的点。 那么,为了将矩形1的坐标转换为矩形2的坐标,< code>x和< c

