如何找到覆盖另一个矩形的矩形区域

Question

我有一个点[xmin，ymin，xmax，ymax]的列表，每个点都按黑点显示

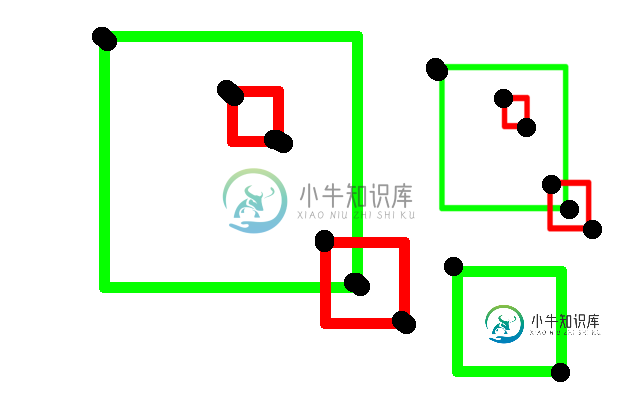
请注意，有许多这样的矩形，如图像所示。红色的应检测删除，绿色的应保留。

输入是 n 矩形 输出是覆盖区域和它覆盖的矩形 id 。最好给出一些算法和解释。

Answer 1

这不是一个答案，只是一个暗示：

您可能会发现四叉树空间细分数据结构非常有用。如果布置得好，那么你可以大大减少碰撞检测的数量。

这种结构被各种2D精灵引擎在旧的街机视频游戏机中使用，它在图形方面也有其他应用。

您的问题看起来就像搜索高效的2D sprite引擎。在电子游戏中，点集经常变化（精灵到处飞），因此算法必须快速。

如果你的任务可以简化为这个问题，那么你应该能够找到许多不同语言的现有代码。

Answer 2

假设矩形列表是< code>L，最后只有绿色矩形的列表是< code>G。可以将矩形一个接一个地添加到G中。每次添加之前，都会对照< code>G中的列表进行检查。如果它与其中一个重叠，比较它们的大小(面积)。如果它大于列表中的值，则替换它，否则不添加到< code>G中。

< code>G永远不会有两个重叠的矩形(这是算法不变量)。这样，您只需检查那些最终出现在最终列表中的候选人。

如果矩形有随机重叠，这肯定比O（n^2）好。但最坏的情况仍然是O（n^2）-当＜code＞L＜code＞中的所有输入矩形都不重叠时。在这种情况下，每个重叠检查都是O（n）操作。

但是可以优化重叠检查。通过维护基于X和Y的点的排序列表，可以仅对最接近矩形的xmin、xmax、ymin和ymax的点进行重叠检查。我认为这有点棘手，尤其是当新矩形仅部分重叠或与多个矩形重叠时。但这是可以做到的。

在任何情况下，重叠检查都可以在一定程度上加速，不必针对< code>G中的所有矩形。我无法量化它，但如果做得正确，我相信，它可以在O(nlogn)中完成。