找到两个覆盖所有点的最小面积的矩形
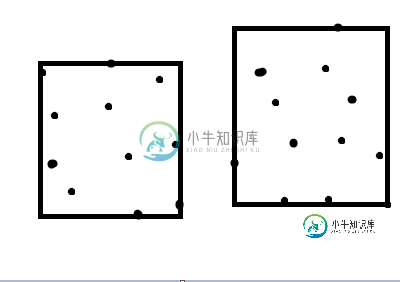
这应该是正确的:
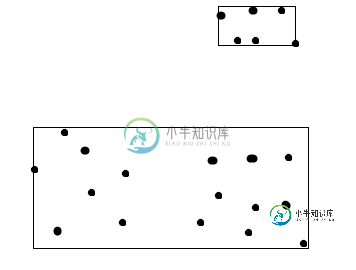
共有2个答案
第一个观察结果是,矩形的任何边都必须接触其中一个点。不接触点的边缘可以向后拉,从而减少面积。
给定n个点,left1、right1、bottom1、top1、left2、right2、bottom2和top2总共有n个选择。这已经给出了一个简单的O(n^8)算法:尝试所有可能的赋值,记住总面积最小的那个(右1-左1)(top1-底部1)(右2-左2)(top2-底部2)。事实上,你可以跳过任何右键组合
另一个观察结果是,边缘应保持在所有点的最小和最大X和Y边界内。找到任意点的最小和最大X和Y值。把这些叫做minX,maxX,minY和maxY。至少有一个矩形需要在这些级别上分别具有左、右、下和上边缘。
因为minx、maxX、minY和maxY必须分配给这两个矩形中的一个,并且有2^4=16种方法可以实现这一点,所以您可以尝试四种可能的分配,其余的坐标分配如上所述。这给出了一个O(n^4)算法:O(n)得到minX、maxX、minY和maxY,然后O(n^4)为八个边坐标的16个minX、maxX、minY和maxY赋值中的每一个填充四个未赋值变量。
到目前为止,我们忽略了矩形不重叠的要求。为了适应这种情况,我们必须确保以下四个条件中至少有一个是正确的:
- Y坐标h与top1之间的水平线
当且仅当这四个条件同时为假时,两个矩形重叠。这允许我们跳过候选解,给出加速,但不改变渐近界O(n^4)。注意,我们需要特别检查这个条件,否则,最优解可能会有重叠(练习:展示这样一个例子)。
让我们试着多花点时间。根据上面的条件#1,假设我们有不重叠的矩形。然后h有n个选择;我们可以尝试这n个选择中的每一个,然后通过找到结果一半中点的最小和最大坐标来确定结果选择的区域。通过尝试h的所有n个选择,我们可以确定“最佳情况”垂直分割。我们不需要尝试条件#2,因为唯一的区别是矩形的顺序是任意的。我们还必须尝试条件#3与水平分裂。这表明一个O(n^2)算法:
- 对于每个点,选择h=point. y
- 用point. y将点分成组
我们能做得更好吗?这是O(n^2)而不是O(n),因为对于h和w的每个选择,我们需要找到每个子群的最小和最大坐标。这假设通过两个子组进行线性扫描。当水平/垂直扫描时,我们实际上不需要对最小和最大X/Y坐标这样做,因为这些都是已知的。我们需要的是解决这个问题的办法:
给定n个点和一个值h,求其Y坐标不大于h的任何点的最大X坐标。
我在上面给出的一个明显的html" target="_blank">解决方案是O(n^2),但是你可以通过巧妙的排序应用找到O(n logn)解决方案,或者甚至可以通过一些更聪明的方法找到O(n)解决方案。我不会尝试这样做。
我们的解是O(n^2);理论上的最优解是ω(n),因为你必须至少看所有的点。所以我们非常接近,但仍有改进的空间。
这两个矩形不能重叠,因此一个必须完全向右或位于另一个的顶部。你的想法是按x值对点进行排序,并找出最大的差距,这很好,但你应该按照你的建议,在两个方向上都这样做。这将在你的例子中找到正确的矩形。
然而,最大的差距不一定是理想的分裂点。根据边界框在垂直方向上的范围,分裂可能在其他地方。考虑一个有四个象限的矩形区域,其中两个对角相对的象限填充有点:
在这里,理想的分割不是最大的差距所在。
通过考虑相邻x坐标和y坐标点之间所有可能的分裂,您可以找到理想的位置。
- 按x坐标对点进行排序
- 按升序扫描已排序的数组。通过存储最小和最大y坐标,跟踪当前点左侧的最小矩形。为每个点存储这些连续的顶部和底部边框
- 现在按降序执行同样的操作,继续运行右矩形的顶部和底部边框
- 最后,再次循环遍历这些点,并计算两个相邻节点之间分割的左、右最小矩形的面积。记录最小面积总和
然后对最小的顶部和底部矩形执行相同的操作。最后两个步骤可以结合使用,这将为右矩形的最小边界保存html" target="_blank">数组。
时间上应该是O(n·log n):排序是O(n·log n),单个通道是O(n)。您需要O(n)额外的内存来运行第一个矩形的边界框。
-
我正在做一个与计算几何有关的个人项目。标题中的问题是对一个小子问题的抽象,我正在努力,但正在努力有效地解决。希望它足够普遍,也许不仅仅是我! 想象一下,我们在平面中有一组S矩形,所有这些矩形的边都平行于坐标轴(没有旋转)。对于我的问题,我们假设矩形交集非常普遍。但它们也非常好:如果两个矩形相交,我们可以假设其中一个总是完全包含另一个。因此,没有“部分”重叠。 我想以以下方式存储这些矩形: 我们可以
-
我们希望您能够帮助我们解决以下问题: 给出了一个可能包含圈的有向图。必须找到一组满足以下标准的路径: 在从节点A到节点B的过程中可以通过的所有边必须被集合内的路径覆盖(一条边可以是集合中多条路径的一部分) 解决方案不必是路径数最少的解决方案,路径也不必是最短的。然而,该解决方案应该可以像java一样使用编程语言高效地实现。我们需要解决方案来生成几个测试用例,覆盖节点a和节点B之间的所有边很重要。
-
我试图解决的问题是: 给定平面上可以以圆为中心的M个点的集合和N个需要被圆覆盖的线段的集合,求线段的最小面积圆覆盖。也就是说,求圆和中心(从M个点中选择)的半径,使得所有N条线段都被覆盖,圆的总面积最小化。 任何指向论文、代码或近似算法的指针都会很棒。
-
将求解第一个点的第一个圆放置在适当位置。 通过检查这两个点之间的距离是否小于2*r来求解最小圈数中的第二个点。并继续处理所有n个点。我认为是贪婪算法,但它是最优的,线性的吗?
-
这是一个面试问题。 我们被赋予各种矩形的尺寸,我们必须找出可以包围所有矩形的矩形面积(最小值)?矩形也可以旋转。 在将矩形拟合到最小可能区域之前,我曾问过一个类似的问题。 上述方法考虑了所有可能性、旋转,并在所有布局情况下确定了所有此类可能性的最小值<我们不能先求矩形面积之和,然后再求最大长度、最大宽度吗?
-
我在leetcode中遇到了一个名为“二叉树相机”的问题。 我在想如何处理这个类似的问题:- 你必须把摄像机放在一个图的节点上,这样整个图就被覆盖了。一个节点上的摄像机监视它的所有近邻节点和它自己。找到覆盖所有节点所需的最小摄像机数量。

