查找覆盖查询点的最小面积矩形

Question

我正在做一个与计算几何有关的个人项目。标题中的问题是对一个小子问题的抽象，我正在努力，但正在努力有效地解决。希望它足够普遍，也许不仅仅是我！

想象一下，我们在平面中有一组S矩形，所有这些矩形的边都平行于坐标轴（没有旋转）。对于我的问题，我们假设矩形交集非常普遍。但它们也非常好：如果两个矩形相交，我们可以假设其中一个总是完全包含另一个。因此，没有“部分”重叠。

我想以以下方式存储这些矩形：

• 我们可以有效地添加新的矩形。
• 给定一个查询点（x，y），我们可以有效地报告包含该点的最小区域的矩形。

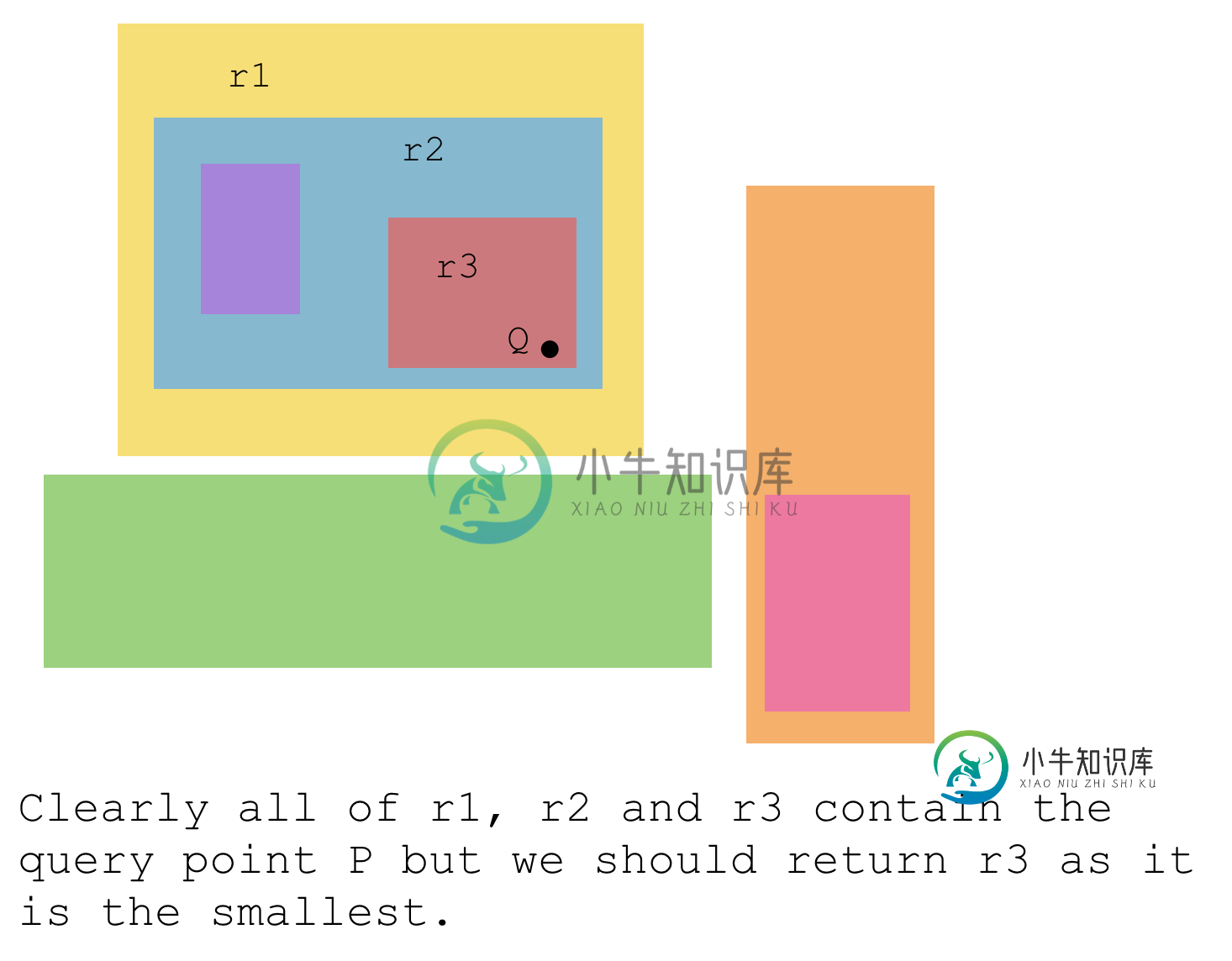
插图为后者提供了动机。我们总是希望找到包含查询点的嵌套最深的矩形，因此它总是面积最小的矩形。

因此，我知道R树和四棵树都经常用于空间索引问题，实际上两者在某些情况下都可以很好地工作。R-Trees的问题在于，在最坏的情况下，它们会降级为线性性能。

我想过基于嵌套性构建一组平衡的二叉树。节点 r 的左子树包含矩形 r 内的所有矩形。右侧子树包含 r 所在的所有矩形。图示的示例将有三棵树。

但是如果没有一个矩形是嵌套的呢？然后你需要O(n)个1元素的树，同样，我们有一些东西的表现和通过盒子的线性扫描一样差。

我如何解决这个问题，在最坏的情况下，我们有渐近次线性时间？即使这意味着在最好的情况下或存储要求下牺牲一些性能。(我假设对于这样的问题，可能需要维护两个数据结构，这很酷)

我确信，允许矩形相交的非常具体的方式应该有助于使这个问题成为可能。事实上，对我来说，它看起来像是对数性能的候选者，但我只是没有任何进展。

提前感谢您的任何想法！

Answer 1

几乎任何索引都可以降级到最坏情况下的O（n）。

问题是你是否会有这样的有害数据，以及你是否针对最坏情况或真实数据进行了优化。

考虑 n 个大小相同、重叠的矩形和交叉点中的一个点...在这里，您将没有太多机会进行优化。

R树是一个非常好的选择。您可以执行优先级搜索，并首选较小的矩形。

但是，您的草图表明您的矩形通常可能是嵌套的，而不是重叠的。标准的 R 树不能很好地处理这个问题。相反，您可能需要修改 R 树以完全使用此结构，并仅将嵌套矩形存储为父级的一部分。

Answer 2

您可以沿着矩形的边缘将区域从xMin到xMax和yMin到yMax进行分区。这最多给出（2n-1）^2个字段。每个字段要么完全为空，要么被可见的（单个矩形的一部分）占据。现在您可以轻松创建一个带有指向顶部矩形的链接的树结构（例如，计算x和y方向的分区数量，其中中间有更多的分区并创建一个节点......递归进行）。因此查找将采用O（log n^2），这是次线性的。并且数据结构需要O（n^2）空间。

在复杂性方面，这是一个更好的实现，因为索引的搜索可以分开，无论矩形的配置如何，对顶部矩形的搜索都只有O（log n），并且实现起来相当简单：

private int[] x, y;
private Rectangle[][] r;

public RectangleFinder(Rectangle[] rectangles) {
    Set<Integer> xPartition = new HashSet<>(), yPartition = new HashSet<>();
    for (int i = 0; i < rectangles.length; i++) {
        xPartition.add(rectangles[i].getX());
        yPartition.add(rectangles[i].getY());
        xPartition.add(rectangles[i].getX() + rectangles[i].getWidth());
        yPartition.add(rectangles[i].getY() + rectangles[i].getHeight());
    }
    x = new int[xPartition.size()];
    y = new int[yPartition.size()];
    r = new Rectangle[x.length][y.length];
    int c = 0;
    for (Iterator<Integer> itr = xPartition.iterator(); itr.hasNext();)
        x[c++] = itr.next();
    c = 0;
    for (Iterator<Integer> itr = yPartition.iterator(); itr.hasNext();)
        y[c++] = itr.next();
    Arrays.sort(x);
    Arrays.sort(y);
    for (int i = 0; i < x.length; i++)
        for (int j = 0; j < y.length; j++)
            r[i][j] = rectangleOnTop(x[i], y[j]);
}

public Rectangle find(int x, int y) {
    return r[getIndex(x, this.x, 0, this.x.length)][getIndex(y, this.y, 0, this.y.length)];
}

private int getIndex(int n, int[] arr, int start, int len) {
    if (len <= 1)
        return start;
    int mid = start + len / 2;
    if (n < arr[mid])
        return getIndex(n, arr, start, len / 2);
    else
        return getIndex(n, arr, mid, len - len / 2);
}

Answer 3

我建议按嵌套层次存储矩形，并按层次处理矩形查找。一旦找到了该点所在的顶级矩形，就可以查看该矩形内的第二级矩形，使用相同的方法找到该点所在的矩形，然后查看第三级矩形，依此类推。

为了避免最坏的情况 O（n） 来查找矩形，您可以使用一种三元空间树，在空间中反复绘制一条垂直线，并将矩形分为三组：左侧（蓝色）、与矩形相交的矩形（红色）和右侧（绿色）的矩形。对于相交矩形组（或者一旦垂直线与大部分或全部矩形相交），请切换到水平线并将矩形划分为线上方、相交和下方的组。

然后，您将反复检查该点是在直线的左侧/右侧还是上方/下方，并继续检查同侧的矩形以及与直线相交的矩形。

在本例中，实际上只需要检查四个矩形，以确定哪个矩形包含该点。

如果我们对示例中的矩形使用以下编号:

那么三元空间树将是这样的：