我如何用最小的节点量覆盖一个图的所有边?
我被一个NP问题困了几天,我正在寻找新的方法来看待这个问题。
这个城市有360个安全摄像头,需要放置在城市的所有街道路口。这个想法是寻找最小数量的摄像头,需要放置,以便有所有的街道覆盖。
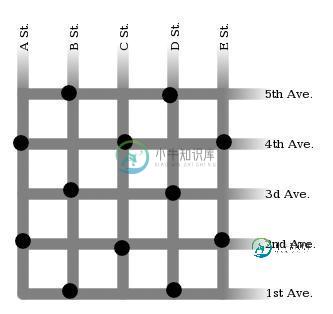
我把每个交叉口都看成是图节点,而街道则是边,最初我认为这是某种中国邮递员问题,但如果你想从一个起始节点出发,覆盖所有边,然后返回到初始节点,那么这个算法主要是有效的。
共有1个答案
通过选择最小数量的顶点覆盖图中的所有边是(最小)顶点覆盖问题。这是一个NP完全问题,所以解决一般情况的最著名算法需要指数时间。(就像所有NP完全问题一样,它也在NP中,但这在这里并不是一个有用的描述,因为许多简单问题也是如此。)
然而,图的某些子类可以更快地求解。二分图就是这样一个类,而网格图(或其子图)是二分的,所以你很幸运。对于网格图,坐标和为偶数的顶点(图中的黑点)构成分区中的一部分,坐标和为奇数的顶点构成另一部分:注意同一部分内的顶点之间没有边。通过使用Hopcroft-Karp算法首先找到最大基数二分匹配,例如在O(E*sqrt(V))时间内找到最小顶点覆盖,然后应用该算法可以找到最小顶点覆盖。
-
我在leetcode中遇到了一个名为“二叉树相机”的问题。 我在想如何处理这个类似的问题:- 你必须把摄像机放在一个图的节点上,这样整个图就被覆盖了。一个节点上的摄像机监视它的所有近邻节点和它自己。找到覆盖所有节点所需的最小摄像机数量。
-
这应该是正确的:
-
将求解第一个点的第一个圆放置在适当位置。 通过检查这两个点之间的距离是否小于2*r来求解最小圈数中的第二个点。并继续处理所有n个点。我认为是贪婪算法,但它是最优的,线性的吗?
-
我试图解决一个问题,其中有一个带正加权边的无向图,我需要找到一个最短的路径,该路径正好覆盖所有节点,一旦给定了起始节点和结束节点。此外,图是完整的(每个节点都连接到图中的所有其他节点)。我已经试着寻找一个算法可以解决这个问题,但我还没有找到一个解决这个问题。由于起止节点的限制,这并不完全是旅游销售员的问题。我将感谢任何帮助。
-
我们希望您能够帮助我们解决以下问题: 给出了一个可能包含圈的有向图。必须找到一组满足以下标准的路径: 在从节点A到节点B的过程中可以通过的所有边必须被集合内的路径覆盖(一条边可以是集合中多条路径的一部分) 解决方案不必是路径数最少的解决方案,路径也不必是最短的。然而,该解决方案应该可以像java一样使用编程语言高效地实现。我们需要解决方案来生成几个测试用例,覆盖节点a和节点B之间的所有边很重要。
-
我试图找出一种算法来寻找二部图的最小顶点覆盖。 我在考虑一个解决方案,将问题简化为二部图中的最大匹配。众所周知,可以使用从bip创建的networ中的最大流量来找到它。图表 最大匹配M应该决定最小。顶点覆盖C,但我无法处理选择要设置C的顶点。假设bip。图有部分X、Y,作为最大匹配边endpoint的顶点在集合A中,那些不属于B的顶点。 我会说,我应该为M到C中的边选择一个顶点。特别是M中的边e的

