有向无环图中的最小路径覆盖
我在这里要问的问题以前在堆栈溢出中已经被问过了。但我无法正确理解Skiminok发布的解决方案。
这是链接。
我尝试了上面链接上发布的解决方案,并给出了两个示例测试用例,但我无法得到正确的答案。
对于测试用例 1::
N=3 和 K=2
5 4 7
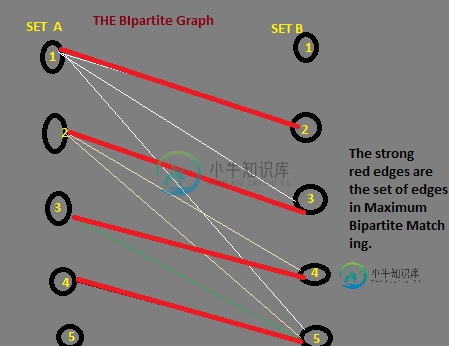
DAG将会是:

注:我构建上述DAG时考虑到:
设pi和pj是两个不同的问题。然后,我们将从pi到pj绘制一条有向边,当且仅当pj可以在pi之后的同一天连续求解。即,必须满足以下条件:
我
|vi - vj|
然后,我构建了二分图,考虑:
对于原始 DAG 的每个有向边 (u, v),应向二分图添加一个无向边 (au, bv),其中 {ai} 和 {bi} 是大小为 n 的两个部分。

答案 =上述二分图中的最大基数匹配。
上述二分图中的最大基数匹配 = 1(绿色 egde)
但答案是2。
类似地,样本测试案例2:
5 1
5 3 4 5 6

上图中的 MAx 基数是多个,但正确答案是 1。
我认为我没有正确地实现它,请你告诉我哪里出错了或者有其他方法吗
谢谢
共有1个答案
我自己找到了答案,第二天就发了这个问题。
我的解决方案通过了所有测试用例。
我在最后一步犯了错误。实际上,答案/解是 SET B 中不包含最大二分匹配边缘的顶点总数。
例如,样本测试用例1:
最大匹配 m={(1A,3B)}.
在两个顶点(顶点1和顶点2)上没有最大匹配的边。所以答案等于这样的顶点的数量=2
对于测试案例2:
最大匹配M={(1A,2B),(2A,3B),(3A,4B),(4A,5B)}。
最大匹配的边不会入射到一个顶点(顶点 1)上。所以答案等于1
-
我想在有向(无环)图中找到最长的路径。假设我知道起始节点-汇。路径应该从这一点开始。我在想我可以将边的权重设置为-1。有很多方法可以找到所有最短的路径,但你必须通过终点。有没有可能得到最短的路径(无论最终节点如何)? 假设我想为节点 nr 1(汇)找到最长路径。所以这个算法给了我1-2-3-4-5-6。
-
我试图将这个问题概念化,然后为它编写Java代码。我知道这里有一些讨论,但我没有看到很多回答者,所以我想通过写下我的想法来重申这个问题,我希望从你们那里得到一些反馈。谢谢 我的想法:对于每个叶节点,找到从根节点到它的最长路径。对于所有路径,找到最大路径长度 然而,这不就是蛮力吗,对此还有更优雅的解决方案吗? 我听说过使用Djikstra的负权重算法,但在某些地方它说这只适用于特定情况?我也看到了关
-
我需要为一组有向无环图找到从节点 0 开始的最长路径。我正在使用维基百科中的最长路径问题算法。我已经让算法适用于大多数图形,但对于其他图形,它没有给出正确的结果。算法为: 图形实现使用邻接列表来存储图形。如果我传递一个图,例如: 我得到的答案5,这是正确的。但是,如果我通过图表: 然后我得到2,而正确答案应该是3。 我使用的TopSort2算法是: DFS 算法包括:
-
在正加权有向无环图中,我有一个求最短路径的问题,但有最大N步(路径中的边)的限制。假定路径存在。图的另一个性质是,如果边(i,j)在图中,那么对于i 例如,考虑下图。 问题是最多使用k=3步(边)来寻找最短路径。答案是6(路径1->4->5->6)。
-
给出了一个边上具有任意权的有向无环图和两个特定结点s和t,其中s的内度和t的外度为0。如何确定成本为正的s到t的最短路径?

