计算一个圆重叠的多个正方形面积的分数

Question

这是一个基于我的编程问题的几何问题。基本上，我有一个充满经纬度点的MySQL数据库，每个经纬度点间隔为1km，对应于每个点周围平方公里内居住的人口。然后，我想知道，这些网格中每一个的相对分数，被一个任意大小的圆圈所占，这样我就可以计算出，在一个给定的圆圈内，大致住着多少人。

以下是问题的一种形式（距离不按比例）的一个实际例子：

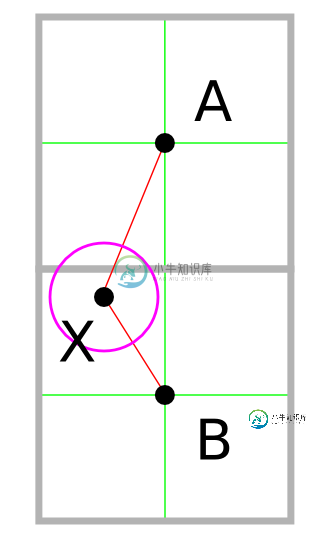
我想知道居住在X点半径内的人口数量。我的数据库计算出a点和B点的条目与X点足够接近，因此是相关的。本例中的A点类似于40.7458，-74.0375，而B点类似于40.7458，-74.0292。从A和B到网格边缘的每条绿线代表0.5公里，因此A和B周围的灰色圆圈分别代表1公里^2。

所以我的问题是：什么是计算网格a的分数和网格B的分数的可靠方法？

最终，我会把人口总数乘以这个分数。所以在这种情况下，周围1km^2的网格对应9561人，B周围的网格是10763人。所以，如果我知道（只是假设）X周围的半径覆盖了A的1%和B的3%，我就可以通过将A和B的人口乘以它们各自的分数，并将它们相加，对这个圆覆盖的总人口做出合理的包络后估计。

我只使用了上面的两个正方形，但根据半径的大小（可以是任意的），可能会有一大堆可能的正方形，就像这样，这使得它成为一个更普遍的问题：

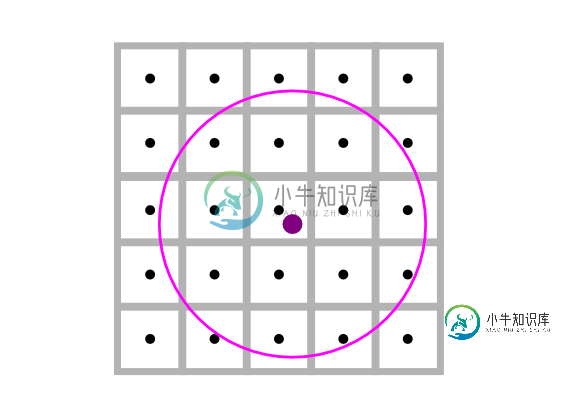
谢谢你的帮助。

Answer 1

我想，我最终想出了一个相当好的近似解决方案。以下是它在PHP中的外观：

//$p is an array of latitude, longitude, value, and distance from the centerpoint 
//$cx,$cy are the lat/lon of the center point, $cr is the radius of the circle
//$pdist is the distance from each node to its edge (in this case, .5 km, since it is a 1km x 1km grid)

function sum_circle($p, $cx, $cy, $cr, $pdist) {
    $total = 0; //initialize the total
    $hyp = sqrt(($pdist*$pdist)+($pdist*$pdist)); //hypotenuse of distance

    for($i=0; $i<count($p); $i++) { //cycle over all points
        $px = $p[$i][0];    //x value of point
        $py = $p[$i][1];    //y value of point
        $pv = $p[$i][2];    //associated value of point (e.g. population)
        $dist = $p[$i][3];  //calculated distance of point coordinate to centerpoint

        //first, the easy case — items that are well outside the maximum distance
        if($dist>$cr+$hyp) { //if the distance is greater than circle radius plus the hypoteneuse
            $per = 0; //then use 0% of its associated value
        } else if($dist+$hyp<=$cr) { //other easy case - completely inside circle (distance + hypotenuse <= radius)
            $per = 1; //then use 100% of its associated value
        } else { //the edge cases
            $mx = ($cx-$px); $my = ($cy-$py); //calculate the angle of the difference
            $theta = abs(rad2deg(atan2($my,$mx)));
            $theta = abs((($theta + 89) % 90 + 90) % 90 - 89); //reduce it to a positive degree between 0 and 90
            $tf = abs(1-($theta/45)); //this basically makes it so that if the angle is close to 45, it returns 0, 
                                      //if it is close to 0 or 90, it returns 1
            $hyp_adjust = ($hyp*(1-$tf)+($pdist*$tf)); //now we create a mixed value that is weighted by whether the
                                                        //hypotenuse or the distance between cells should be used                                                   

            $per = ($cr-$dist+$hyp_adjust)/100; //lastly, we use the above numbers to estimate what percentage of 
                                                //the square associated with the centerpoint is covered
            if($per>1) $per = 1; //normalize for over 100% or under 0%
            if($per<0) $per = 0; 
        }
        $total+=$per*$pv;   //add the value multiplied by the percentage to the total
    }  
    return $total;
}

这似乎是有效的，而且非常快（尽管它确实在边缘情况下使用了一些触发）。基本逻辑是，当计算边缘情况时，两种极端的可能性是圆半径要么正好垂直于网格，要么正好与网格成45度角。因此，它大致计算出在这些极值之间的位置，然后用它大致计算出网格正方形被覆盖的百分比。它在我的测试中给出了可信的结果。

对于我使用的正方形和圆形的大小，这似乎足够了？