消除孤立顶点并重新排序结果图顶点的有效方法

Question

对于一个头衔来说，这真是太多了，但接下来就是。我面临的问题是从输入流中读取一组无向边和一些顶点，然后输出一组边。我输出的边集不能有任何“空白”——我的意思是，我不能有一个（1,2）、（2,4）和（4,5）的边集，因为顶点集中永远不会提到3。

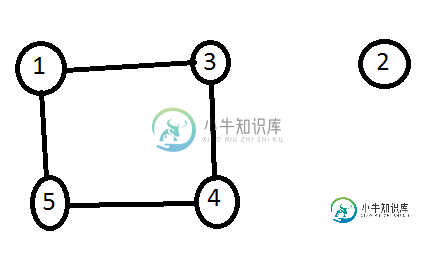
这个图是不允许的，因为2是“空白”

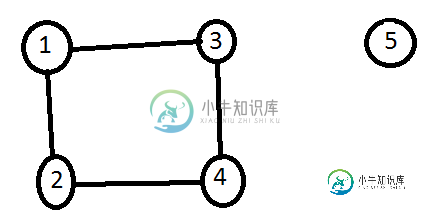
此图是允许的，因为连接图中没有“空白”。有4个顶点，编号为1到4。这个图表的输出将是[[1,3][3,4][4,2][2,1]]

到目前为止，我是如何做到这一点的：

当我知道有多少个顶点时，我会将它们的所有索引添加到包含所有孤立顶点的HashSet中。当我从输入流中读取边缘时，我会从HashSet中删除每条边缘的两个顶点。之后，我会将它们添加到一个具有维度（|V|，2）的2D数组中。如果在我接收所有边缘后有任何孤立的顶点，我会调用我的“重新排序方法”。

它的作用如下：

• 将2D矩阵和孤立顶点集作为输入

在伪这是（程序本身是用Java编写的）

reorderMethod(matrix M, isolated vertex set I) 
  matrixProperties = findMatrixProperties(M) // matrixProperties is an instance of a helper class MatrixProperty which holds two integers, max and nrOfVertices
  while (max > nrOfVertices) 
    for row in M
      for col in M 
        if M[col, row] = max:
          M[col, row] = min(I)
    // Remove min(I) from I 
    matrixProperties = findMatrixProperties(M)

我有没有办法让这更有效？

Answer 1

如果我正确理解了你的问题，你想找到一个图的顶点的规范重新编号，这样就没有一个完全未连接的节点比连接的节点有更小的标签。

简单的解决方法是用较小标签连接的顶点数来标记每个顶点。（这将从0开始对顶点进行编号，而不是从1开始，但您可以很容易地为每个标签添加一个顶点。）

您似乎使用的是布尔NxN数组，而不是邻接列表，所以我就是这样编写下面的伪代码的。不过，对邻接列表的更改微不足道。

我们首先通过对每一行应用或运算符，将布尔数组简化为布尔向量。一个节点连接到某个东西，除非它的整行为false，所以布尔向量足以告诉我们一个节点是否连接。显然，当我们点击第一个true值时，我们可以停止扫描一行。然后，我们将布尔向量重新解释为0和1的整数向量，并在向量上做一些非常类似于累积和的事情，这样向量将包含每个条目中具有较小标签的连接组件的数量，这意味着，如果忽略未连接的顶点，生成的向量正是从旧标签到规范标签的转换。（可以为所有顶点构造转换；下面的伪代码将通过重新编号上一个标签下未连接的顶点来实现。）

我使用了类似python的伪代码，因为Java对我来说不够伪：）

# M is an adjacency matrix; we assume that it is square.
# The function returns the translation vector
def renumber(M):
  ones = 0
  zeros = len(M) - 1
  trans = []
  for row in M:
    if any(row):
      # the edge is connected
      trans.append(ones)
      ones += 1
    else:
      # the edge is unconnected
      zeros -= 1
      trans.append(zeros)
  return trans