网格上二维正方形的非间断矩形边覆盖

Question

尽管标题听起来很复杂，但我的实际问题应该不太难建模。但是，我无法找到一个好的算法来执行以下操作：

我想用固定数量的n个矩形覆盖网格上的一组正方形。这些矩形可能会重叠，它们只需要覆盖我的形状的外边缘。

平方米x平方米网格上不同矩形的数量为：

因此，蛮力方法必须尝试的组合数量是

对于10 x 10网格和仅3个矩形，这将是2768064625个组合。

带有一些正方形的初始网格可能如下所示：

n = 1：用单个矩形覆盖此形状的最佳方法是：

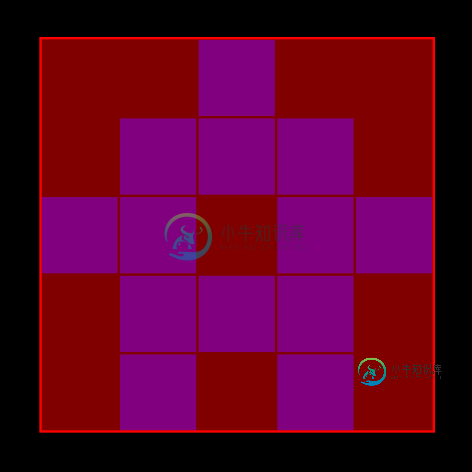
n=2：可以使用以下两个矩形减少被覆盖的空正方形的数量：

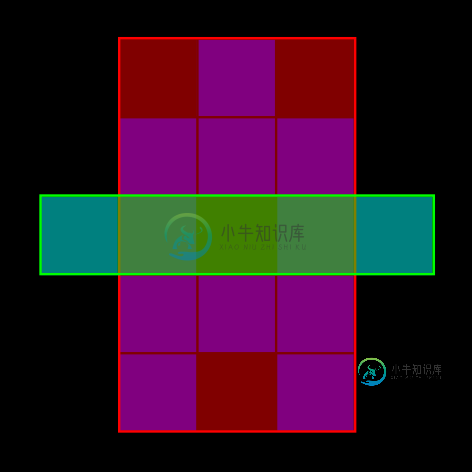
(注意，中心现在被两个矩形覆盖)

我正在寻找一种解决方案，它至少覆盖作为外边缘一部分的所有正方形，即共享网格宽度上一条边的所有填充正方形，即空正方形。

不属于形状的外缘的所有正方形可以或不被覆盖，覆盖的矩形可以或不相交。

给定一个固定数量的覆盖矩形n，我想覆盖所有填充的正方形，但最小化形状外被覆盖的空白正方形的数量。这意味着中间的空方块不应该计入必须最小化的目标函数(我也可以在应用算法之前填充所有的洞，而不会产生差异)。

因此，我的示例的目标函数的值为：

n  |  target function
---|-----------------
1  |  11
2  |   3

请注意，原始的正方形集可能没有连接，并且未连接的子形状的数量甚至可能超过覆盖矩形的数量。

为了简化问题，您还可以只处理输入数据的转换版本：

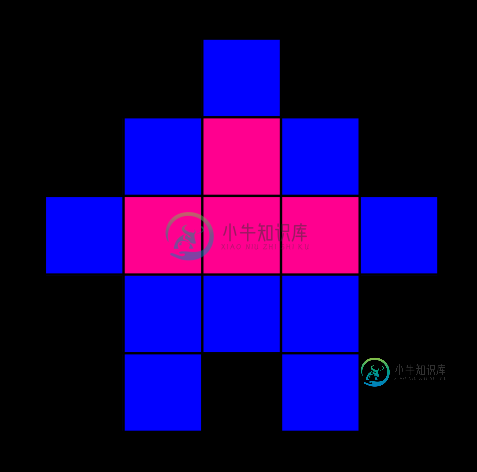
然后目标是覆盖所有蓝色方块，并使用n个可能相交的矩形最小化覆盖的白色方块的数量。

Answer 1

我有一个不同的问题，我想提出：

假设你有三个孤立的正方形，可能性是什么：

一个矩形覆盖所有三个

两个矩形，3种可能性覆盖2 1

和三个各覆盖一个的矩形

所以订单是Sum_i n_choose_i

比您的订单小得多

在任何情况下都是n上的多项式而不是指数。

然后你可以修剪你的解决方案（顺便说一下，这是矛盾的：哪个更好更少的矩形或更少的空单元格，但你可以覆盖它）

Answer 2

嗯，我还没有想到一个P类解，但是我确实想到这个问题可能是随机解的一个很好的候选者。

值得注意的是，有一个容易定义的可行起点：只需将所有覆盖矩形设置为目标正方形边界框的范围。

从这个初始状态，可以通过减少覆盖矩形的一个边界并检查所有目标正方形是否仍被覆盖来生成新的有效状态。

此外，任何两个状态之间的路径可能很短（每个矩形都可以在O（√n）时间内减小到其适当的尺寸，其中n是边界框中的平方数），这意味着在搜索空间中很容易移动。虽然这需要注意的是，一些可能的解决方案被一条回到初始状态的狭窄路径隔开，这意味着重新运行我们即将开发的算法几次可能是好的。

鉴于上述情况，模拟退火是解决问题的可能手段。以下 Python 脚本实现了它：

#!/usr/bin/env python3

import random
import numpy as np
import copy
import math
import scipy
import scipy.optimize

#Generate a grid
class Grid:
  def __init__(self,grid_array):
    self.grid    = np.array(grid_array)
    self.width   = len(self.grid[0]) #Use inclusive coordinates
    self.height  = len(self.grid)    #Use inclusive coordinates
    #Convert into a list of cells
    self.cells = {}
    for y in range(len(self.grid)):
      for x in range(len(self.grid[y])):
        self.cells[(x,y)] = self.grid[y][x]
    #Find all cells which are border cells (the ones we need covered)
    self.borders = []
    for c in self.cells:
      for dx in [-1,0,1]:                #Loop through neighbors
        for dy in [-1,0,1]:
          n = (c[0]+dx,c[1]+dy)          #This is the neighbor
          if self.cells[c]==1 and self.cells.get(n, 1)==0: #See if this cell has a neighbor with value 0. Use default return to simplify code
            self.borders.append(c)
    #Ensure grid contains only valid target cells
    self.grid = np.zeros((self.height,self.width))
    for b in self.borders:
      self.grid[b[1],b[0]] = 1
    self.ntarget = np.sum(self.grid)
  def copy(self):
    return self.grid.copy()

#A state is valid if the bounds of each rectangle are inside the bounding box of
#the target squares and all the target squares are covered.
def ValidState(rects):
  #Check bounds
  if not (np.all(0<=rects[0::4]) and np.all(rects[0::4]<g.width)): #x
    return False
  if not (np.all(0<=rects[1::4]) and np.all(rects[1::4]<g.height)): #y
    return False
  if not (np.all(0<=rects[2::4]) and np.all(rects[2::4]<=g.width)): #w
    return False
  if not (np.all(0<=rects[3::4]) and np.all(rects[3::4]<=g.height)): #h
    return False
  fullmask = np.zeros((g.height,g.width))
  for r in range(0,len(rects),4):
    fullmask[rects[r+1]:rects[r+3],rects[r+0]:rects[r+2]] = 1
  return np.sum(fullmask * g.grid)==g.ntarget

#Mutate a randomly chosen bound of a rectangle. Keep trying this until we find a
#mutation that leads to a valid state.
def MutateRects(rects):
  current_state = rects.copy()
  while True:
    rects = current_state.copy()
    c = random.randint(0,len(rects)-1)
    rects[c] += random.randint(-1,1)
    if ValidState(rects):
      return rects

#Determine the score of a state. The score is the sum of the number of times
#each empty space is covered by a rectangle. The best solutions will minimize
#this count.
def EvaluateState(rects):
  score   = 0
  invgrid = -(g.grid-1) #Turn zeros into ones, and ones into zeros
  for r in range(0,len(rects),4):
    mask = np.zeros((g.height,g.width))
    mask[rects[r+1]:rects[r+3],rects[r+0]:rects[r+2]] = 1
    score += np.sum(mask * invgrid)
  return score

#Print the list of rectangles (useful for showing output)
def PrintRects(rects):
  for r in range(0,len(rects),4):
    mask = np.zeros((g.height,g.width))
    mask[rects[r+1]:rects[r+3],rects[r+0]:rects[r+2]] = 1
    print(mask)



#Input grid is here
gridi = [[0,0,1,0,0],
         [0,1,1,1,0],
         [1,1,0,1,1],
         [0,1,1,1,0],
         [0,1,0,1,0]]

g = Grid(gridi)

#Number of rectangles we wish to solve with
rect_count = 2

#A rectangle is defined as going from (x,y)-(w,h) where (w,h) is an upper bound
#on the array coordinates. This allows efficient manipulation of rectangles as
#numpy arrays
rects = []
for r in range(rect_count):
  rects += [0,0,g.width,g.height]
rects = np.array(rects)

#Might want to run a few times since the initial state is something of a
#bottleneck on moving around the search space
sols = []
for i in range(10):
  #Use simulated annealing to solve the problem
  sols.append(scipy.optimize.basinhopping(
    func      = EvaluateState,
    take_step = MutateRects,
    x0        = rects,
    disp      = True,
    niter     = 3000
  ))

#Get a minimum solution and display it
PrintRects(min(sols, key=lambda x: x['lowest_optimization_result']['fun'])['x'])

这是我在上面的示例代码中指定的十次运行的算法进度，作为迭代次数的函数（我添加了一些抖动，以便您可以看到所有行）：

你会注意到，大多数（8/10）的运行在早期找到8的最小值。同样，在6/10的运行中，发现5的最小值，大多数运行在早期。这表明，运行许多较短的搜索可能比运行几个较长的搜索更好。选择合适的长度和运行次数将是一个实验问题。

请注意，每次空正方形被矩形覆盖时，EvalateState都会加点。这会抑制找到解决方案所需的冗余覆盖，或者可能导致更快地找到解决方案。成本函数包含此类内容是很常见的。尝试直接询问您想要什么的代价函数很容易——只需将EvalateState替换如下：

#Determine the score of a state. The score is the sum of the number of times
#each empty space is covered by a rectangle. The best solutions will minimize
#this count.
def EvaluateState(rects):
  score   = 0
  invgrid = -(g.grid-1) #Turn zeros into ones, and ones into zeros
  mask = np.zeros((g.height,g.width))
  for r in range(0,len(rects),4):
    mask[rects[r+1]:rects[r+3],rects[r+0]:rects[r+2]] = 1
  score += np.sum(mask * invgrid)
  return score

在这种情况下，使用此成本函数似乎会产生更好的结果：

这可能是因为它为矩形在可行状态之间提供了更多的转换路径。但是如果你遇到困难，我会记住另一个函数。

Answer 3

不是一个完整的解决方案，而是一些（在特定条件下最优保持）约简规则：

>

如果您想要一个完全不覆盖白色正方形的解决方案，那么您可以安全地合并任何相邻的一对相同的行或列。这是因为，任何不覆盖任何白色正方形的较小合并问题的有效解决方案都可以扩展为原始问题的解决方案，方法是按合并执行的相反顺序在每个合并线上“拉伸”每个矩形——这不会导致任何未覆盖的白色正方形被覆盖，任何蓝色正方形被覆盖，或者改变所需矩形的数量。根据原始图像的“曲线”程度，这可能会大大减少输入问题的大小。（即使对于覆盖白色方块的解决方案，您仍然可以应用此策略，但“扩展”解决方案可能会覆盖比原始解决方案更多的白色方块。作为一种启发式方法，此策略仍然有用。）

您可以通过将已放置的矩形（无论它们最初是蓝色还是白色）覆盖的所有单元格变成粉红色来表示任何部分解决方案；粉红色单元格是可以免费被（其他）矩形覆盖但不需要覆盖的单元格。如果您正在寻找一种完全不覆盖白色正方形的解决方案，则可以应用规则1的强化形式来缩小实例：不仅可以像以前一样合并相同的相邻行和列对，还可以根据以下规则首先将一些粉色单元格改为蓝色，这可能会使更多的合并发生。两个相邻列的规则是：如果列1中的每个白色单元格在列2中也是白色的，反之亦然，则在包含一个粉色和一个蓝色单元格的每一行中，可以将粉色单元格更改为蓝色。（理由：某些非白色单元格覆盖矩形最终必须覆盖蓝色单元格；该矩形可以拉伸以覆盖粉色单元格，而不覆盖任何新的白色单元格。）示例：

WW         WW         W
BB         BB         B
BP   -->   BB   -->   B
PP         PP         P
PB         BB         B

您永远不需要考虑一个矩形，它是不覆盖白色单元格的矩形的适当子矩形。

还有一些想法：

只需将图像大小调整为较小的大小，其中新高度是原始高度的整数因子，并且宽度类似，并且单元格是蓝色的，而原始图像中相应单元格块中的任何单元格都是蓝色的，应该给出一个更容易解决的良好近似子问题。（如有必要，请用白色单元格填充原始图像。在解决此较小的问题并将解决方案重新展开到原始大小之后，您可能能够从某些矩形的边缘修剪更多的行或列。