有向无环图的有效遍历

Question

输入：

nd[0];
nd[1, 2];
nd[3, 4];
nd[0, 1];
nd[2, 3];
nd[0, 4];
nd[1, 3];
nd[0, 2];
nd[1, 4];
nd[3];
nd[1, 4];

生成的树：

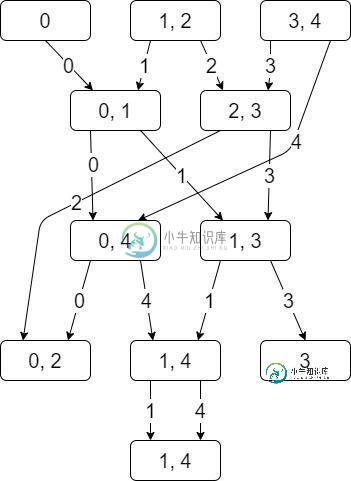
输出：

total_time = sum of all individual wait_time //without overlap

规则：

< li >输入代码总是会产生一个有向无环图 < li >每个节点都有一些wait_time值 < li >完整的图形遍历应该计算整个图形的总等待时间 < li >必须并行遍历所有独立节点(或者至少时间计算应该是这样) < li >如果两个不同节点的wait_time发生重叠，则将考虑最大值，遍历时间较短的节点将移动到下一个独立节点 < li >除了根和叶(可以有多个根和叶)之外，所有单个和成对的节点将正好有1条和2条入边和出边

问题1：如何将给定的输入代码转换为图形，以便可以遍历？（伪代码或任何类型的指导可能会有所帮助）

问题2：如何根据上述规则实现成功的遍历？

以前的努力：

>

我能够使用拓扑排序以线性方式对节点进行排序，但我不确定如何实现这些特定目标。

我根据代码的直觉绘制了这个图。

边缘的数字只是为了澄清导致依赖的数字。

我正在使用python 3

我之前的代码似乎与这些问题没有任何意义，所以我没有包含它。

Answer 1

1. 创建图形

设 a、b、c 三个节点，它们具有 0 属性/共同的解除性（到节点 0）。如果 a 在 b 之前发现，而 b 在 c 之前发现，则边应为 a-

要解决上述规则，请考虑为每个发现的数字设置缓存。如果一个节点包含0，那么您将其缓存为缓存[0]。稍后，如果其他节点b包含0，您必须从缓存[0]到b创建边缘，并更新该缓存，以便包括0的后续节点从b获得边缘。

foreach input as node
  forall dependancy of node
    if discovered[dependancy]
      make_edge(discovered[dependancy], node)
    fi
    discovered[dependancy] = node // apply dependancy "transitivity"

现在，要将图形构建为“层”，您可以从叶子开始（层＜代码＞0 [1,4]。（因为＜code>[1,3]在链接到＜code>[3]时，它是一个叶子，也链接到＜code>[1，4]而不是。因此排除在外）。然后，您构建了层＜code＞1＜/code＞。

构建第n层时，您只能将具有dep的节点添加到第0层到第n-1层

一种更简洁的说法是对一个节点来说，计算它的偏心度（最长的路径（这里到树叶））。

要像您一样打印图形，请注意，您可以通过偏心度绘制节点，这将显示依赖的“级别”（它们距离叶子/末端有多远，请参阅下面代码中的plotByLayers）。

我们不需要像上面那样麻烦地构建层。

节点只能在其所有祖先结束时启动。

祖先在我们做图的时候就已经确定了。

因此，递归是

n.endAt = max(n.endAt for n in n.ancestors) + n.wait

初始化是针对根节点（没有依赖关系）的，我们可以在其中保留等待时间。

nroot.endAt = nroot.wait

关于节点。id表示法＜code＞i）x，y。i是作为读入输入的第i个节点。（不知何故，它的真实id。x，y只是帮助我们可视化的垃圾。）。

const input = `
nd[0];
nd[1, 2];
nd[3, 4];
nd[0, 1];
nd[2, 3];
nd[0, 4];
nd[1, 3];
nd[0, 2];
nd[1, 4];
nd[3];
nd[1, 4];`
function makeGraph(input) {
  const nodes = input.trim().split('\n').map((x,i) => {
    const deps = x.match(/\[(.+)\]/)[1]
    return { id: i+')'+deps, v: deps.split(',').map(x => x.trim()) }
  })
  const edges = {}
  const discovered = {}
  nodes.forEach((node, i) => {
    node.v.forEach(digit => {
      if (discovered[digit]) {
        // there is an edge
        edges[discovered[digit].id] = edges[discovered[digit].id] || []
        edges[discovered[digit].id].push(node)
      }
      // apply transitivity a->b->c
      discovered[digit] = node
    })
  }) 
  return {nodes, edges}
}

function computeEccentricity(n, edges) {
  if (typeof(n.eccentricity) !== 'undefined') {
    return n.eccentricity
  }
  if (!edges[n.id]) {// a leaf has no outgoing edges
    n.eccentricity = 0
    return 0
  }
  const distances = Object.values(edges[n.id]).map(n => computeEccentricity(n, edges))
  const min = Math.max(...distances)
  n.eccentricity = 1 + min
  return n.eccentricity
}

function plotByLayers(nodes) {
  const lvls = []
  let m = 0;
  nodes.forEach(n => {
    const i = n.eccentricity
    lvls[i] = lvls[i] || []
    lvls[i].push(n)
    m = i > m ? i: m
  })
  for(let i = m; i >=0 ; --i) {
    console.log(lvls[i].map(x => x.id))
  }
  return lvls
}
const { nodes, edges } = makeGraph(input)
nodes.forEach(n => computeEccentricity(n, edges))
plotByLayers(nodes)

// for any node, compute its ancestors.
nodes.forEach((n, i) => {
  if (edges[n.id]) {
    edges[n.id].forEach(v => {
      v.ancestors = v.ancestors || []
      v.ancestors.push(n)
    })
  }
  n.wait = 2**i // say arbitrarily that i node waits 2^i some time
})
function computeEndAt(node) {
  if (typeof(node.endAt) !== 'undefined') {
    return node.endAt
  }
  if (!node.ancestors) {
    node.endAt = 0 + node.wait
    return node.endAt
  }
  const maxEnd = Math.max(...node.ancestors.map(computeEndAt))
  node.endAt = maxEnd + node.wait
  return node.endAt
}
nodes.forEach(computeEndAt)
const longest = nodes.sort((a,b)=>b.endAt - a.endAt)[0]
console.log('awaited: ', longest.endAt, longest.id)