从给定“根”的无向无环图创建有向无环图

Question

考虑以下无向非循环图:

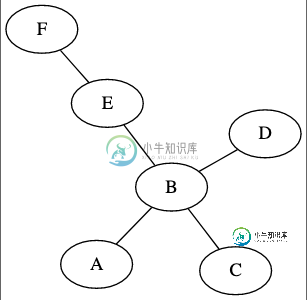
如果我们定义“根”为A和E，有没有算法可以确定产生的有向无环图？：

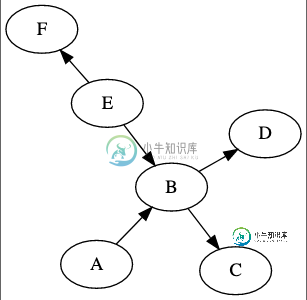
我考虑过从根开始尝试某种DFS或BFS，但我不确定如何处理“等待”的需要，以查看另一个根是否可能到达给定的节点。

Answer 1

我假设你们要找的是边的方向，这样

< li >整个图形是一个DAG，并且 < Li > DAG的源节点就是您指定的节点。

现在，让我们忽略第二个约束。使整个图形成为DAG的一种简单方法是分配一个排序1 ...n 到节点，然后让边始终指向从较低节点到较高节点。因此，问题是如何以一种为您提供第二个属性的方式分配数字。

我相信你可以通过在图上运行BFS，用你的所有k个根节点播种队列来做到这一点。如果您按照节点被发现的顺序对其进行编号，那么您将得到一个DAG(节点的任何顺序都会得到一个DAG)。此外，假设没有两个根是彼此相邻的，并且在图的每个连通分量中至少有一个根，那么你的根将是唯一的根。

为了了解这一点，假设没有一个根是相邻的，并且图是连通的，那么为了矛盾起见，假设另一个节点是根。取编号最低的节点，而不是您选择的也是根的节点之一。因为节点被分配了一个编号，所以它一定是在BFS中发现的，因此它与BFS中也发现的其他编号较低的节点相邻。但是，编号较低的节点的边将有一个箭头指向编号较高的节点，因此它不是根。

（如果有两个相邻的节点要成为根，则无法实现这一点，因为其中一个节点将有一个箭头指向另一个节点。）

总的来说，这在时间O(m n)上运行，因为它只是图上的一个BFS。