Bellman Ford算法能有任意的边序吗？

Question

我刚刚开始学习新的算法，但当我读到贝尔曼·福特关于极客的算法时，我陷入了困境：http://www.geeksforgeeks.org/dynamic-programming-set-23-bellman-ford-algorithm/

那里写着-

该算法以自下而上的方式计算最短路径。它首先计算路径中最多有一条边的最短路径的最短距离。然后，它计算最多有2条边的最短路径，依此类推。

在外环第i次迭代后，计算出最多有i条边的最短路径。在任何简单路径中都可能有最大| V |–1条边，这就是为什么外部循环运行| V |–1次。其思想是，假设没有负权重循环，如果我们已经计算出最多有i条边的最短路径，那么对所有边的迭代保证给出最多有（i1）条边的最短路径。

让我们通过下面的示例图来了解算法。这些图像是从这个来源拍摄的。

让给定的源顶点为0。将所有距离初始化为无限，但与源本身的距离除外。图中的顶点总数为5，因此所有边都必须处理4次。

在下面的例子中，如果边的顺序是-（AB），（BE），（ED），（DC），（AC），（BC），（DB），（BD），那么在只有一次迭代中，它将计算具有甚至2-3条边的最短路径，这与“它首先计算最短距离指路径中最多有一条边的最短路径。然后，它计算最多有2条边的最短路径，依此类推。在外循环的第i次迭代之后，计算最多有i条边的最短路径”，因此在改变边的顺序时，这种说法将被证明是错误的。

让我们通过下面的示例图来了解算法。这些图像是从这个来源拍摄的。

让给定的源顶点为0。将所有距离初始化为无限，但与源本身的距离除外。图中的顶点总数为5，因此所有边都必须处理4次。

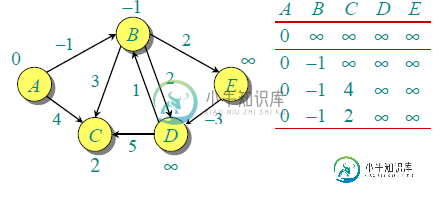
第一次迭代保证给出所有最短的路径，这些路径最多只有一条边长。当第二次处理所有边时，我们得到以下距离（最后一行显示最终值）。

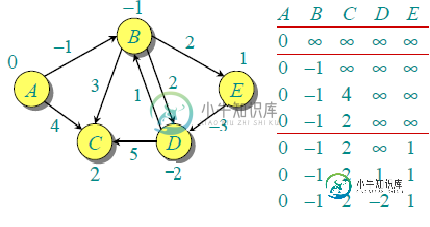
第二次迭代保证给出最多2条边长的所有最短路径。该算法处理所有边缘2次以上。距离在第二次迭代后最小化，因此第三次和第四次迭代不会更新距离。

Answer 1

使用注释引用的表行

第四行显示何时处理（D，C）、（B，C）和（E，D）。

是不正确的。这意味着存在一条从A到C的路径，长度为2，最多包含一条边——然而这样的路径不存在。

Answer 2

那是正确的。放松的顺序并不重要。

有3个节点，所以可以做两次松弛迭代。如果松弛从节点b开始向后发生，然后到节点a，第一次迭代将产生b：无穷大，a： 2。那么第二次迭代是b： 5，a： 2。在第一次迭代中，b不能更新，因为只使用了一条边，所以只能更新距离它一条边的节点a。第二次迭代是当从源到任何地方使用两个边时，所以b最终可以更新。在第一次迭代中，b根本无法更新，因为a还没有准备好。

那么，我们看看正向更新怎么样？在第一次迭代中，它将是a:2和b:5。第二次迭代是a:2和b:5。向前移动可以让所有连续的节点准备好更新的距离，所以更多的迭代不会改变值。但是有人可能会想，如果我对101个节点进行100次迭代，然后进行正向更新，会怎么样。是否有可能在第一次迭代中所有内容都被更新了，并且在第99次迭代之前没有任何更改，并且在第100次迭代时突然有一个节点的距离减小了？不，这是不可能的，因为前向更新不会在第一次迭代后引起更改，除非有一个负循环。

你可以在这里阅读更多关于贝尔曼-福特的信息：https://medium.com/@logicdevildotcom/inetive-编程-应用到图形-f33b6b8a8247

Answer 3

是的，贝尔曼福特的作品无论在哪个顺序的边缘处理。事实上，这就是为什么您必须进行n-1迭代的原因。如果你知道，什么是边的最佳顺序——只有一次迭代就足够了。

考虑以下图表（所有边都有权重1）：

 (1) --> (2) --> (3) --> (4) 

如果按1的顺序处理边-

但是，n-1迭代是最坏的情况，无论边缘的处理顺序如何（如果没有负循环）。