具有双向边图的Ford-Fulkerson算法
我有一些困难理解福特-富尔克森算法的最大流量,希望得到一些帮助。
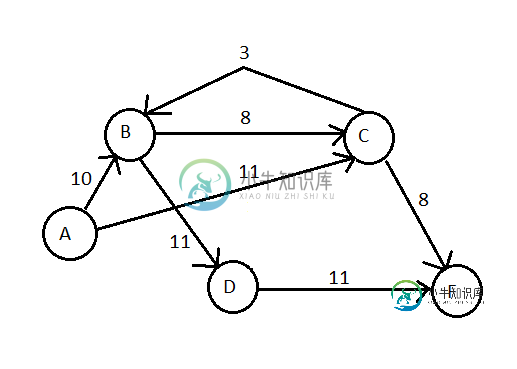
您会注意到节点B和C有一个双向边沿,B-C的容量为8,C-B的容量为3。

现在假设下一条路径是a-c-b-d-f。
我的问题是,我们现在能够通过C-B推动多少流量?是11通过使用8已经推动的流量加上能力3在另一个边缘还是只有3或可能8?
谢谢你抽出时间。
共有1个答案
我认为你错误地构造了第二个残差图。这里是我从第一张图准备的版本。
每当您将一个流传递到一个扩展路径中时,您需要同时调整容量。因此,当您沿着A-B-C-F路径传递值为8的流时,您需要在将下一个流传递到图中之前调整相关边的容量。
因此,值8来自边缘B-C或C-F的瓶颈容量。由于您已经通过了这两个边的最大流量,而您不能通过超过8个,因此您已经最大限度地利用了这些边的容量。这就概括为这样一种想法:每当您使用某些边通过某些流时,您需要绘制后向边,并将流值与后向边的容量相加,然后从前向边中减去。
你可以从我给你的第二张图的版本中看到这一点。由于B-C没有更多的能力来承载额外的流(8-8=0),我省略了边缘,并将能力添加到反向边缘(即C-B,其中能力增加到3+8=11)。同样的事情也发生在C-F身上。
现在对于A-B,由于我们已经通过了8和容量为10的路径,我们还剩下2个容量来通过更多的流。因此,我们从A-B中减去这个值,得到(10-8=2)。我们还添加反向边B-A,该边是通过添加流值(即0+8=8)而创建的。
现在,由于我们已经正确地构建了残差图,剩余的唯一可以承载来自A-F的流的增广路径是流值为2的A-B-D-F(瓶颈容量为2)。
因此,最大流量值(总流量值)为8+2=10
希望有帮助!
-
假设我们重新定义剩余网络,不允许边进入。认为福特-富尔克森的程序仍然正确地计算了最大流量。 我在想,当我们增加一条路径时,反向边缘的剩余容量会增加,如果需要,可以用来减少该边缘的流量(但总体上增加网络流量)。因此,如果我们不允许边进入,这意味着我们不允许边中的流减少(是的相邻节点)。因此,当我们允许边进入时,我们可以有一个类似的循环 但是如果我们再次禁止边进入,我们可以在没有循环的情况下找到相同的
-
我试图在Java实现Ford Fulkerson算法。到目前为止,我有了一个带节点和边的图。节点包含一个ID字符串和一个边的邻接列表。边包含容量和它通向的节点。 我正在尝试理解维基百科页面上的psudo代码,以及如何实现它(我正在使用Java)。这是我目前所理解的: > 首先我将图中所有边的流设置为零。(什么是表示流的好方法?直接在我的图的边中作为变量?) 第二步是创建残差图,它是一个网络,其中边
-
我已经实现了Ford Fulkerson算法,现在正在尝试它的一个变体。 假设解导出后,其中一条边的容量增大或减小。我们需要找到一个算法,以获得新的最大流量使用当前的解决方案,而不是从一开始。 我的建议是,在这个例子中,如果我们假设1-3个边的容量从12减少到8,那么我们需要做一个从1到开始节点的BFS,并且在每个边上减少4的流量,做一个从3到5的BFS,并且减少那里的流量。但我不确定这是否正确。
-
我刚刚开始学习新的算法,但当我读到贝尔曼·福特关于极客的算法时,我陷入了困境:http://www.geeksforgeeks.org/dynamic-programming-set-23-bellman-ford-algorithm/ 那里写着- 该算法以自下而上的方式计算最短路径。它首先计算路径中最多有一条边的最短路径的最短距离。然后,它计算最多有2条边的最短路径,依此类推。 在外环第i次迭代
-
我有一些关于点为双类型的多边形的问题...我要做的是,给定点,创建多边形,然后测试1个具体点是否在多边形内。 所以我知道在Java中有一个类,叫做多边形,用得像这样:(三角形) 但我的“多边形”必须是“双”类型,而不是“int”(简单示例) 在我的项目中,我真的不需要在小程序或类似物上绘制它,我只需要计算点是否在里面。 所以我的问题是: 有没有什么方法可以用双坐标来处理多边形,可以计算这个点(双坐
-
我有一个有向图,边上的权值是非负的。 我的算法应该做到以下几点: 获取从顶点u到顶点V的所有路径 计算从u到v的每条路径上的最小加权边 计算我从上面计算的最小加权边的最大值。

