联合查找不相交路径压缩算法

Question

我这个星期天要参加考试，我只想确认我正在做的事情是否正确（你知道考试让我持怀疑态度）

这就是算法的工作原理：

int Find(int x)
{ // Return the set containing x and compress the path from x to root
  // First, find the root
int z = x; while (P[z] > 0) { z = P[z]; } int root = z;
// Start at x again and reset the parent // of every node on the path from x to root z = x;
while (P[z] > 0)
{ int t = P[z];
     P[z] = root; // Reset Parent of z to root
z = t; }
return root; }

这就是问题所在：

回想一下为不相交集开发的算法，这些不相交集来自一组n个元素。查找使用路径压缩，联合使用排名。此外，相同等级的两棵树的联合选择与第二个参数关联的根作为新根。从一个集合S={1,2，…，10}和10个不相交子集开始，每个子集都包含一个元素。a.执行后绘制最后一组树：
Union（1,2）， Union（3,4）， Union（5,6）， Union（1,5）， Union（1,3）。

这是我对这个问题的回答：

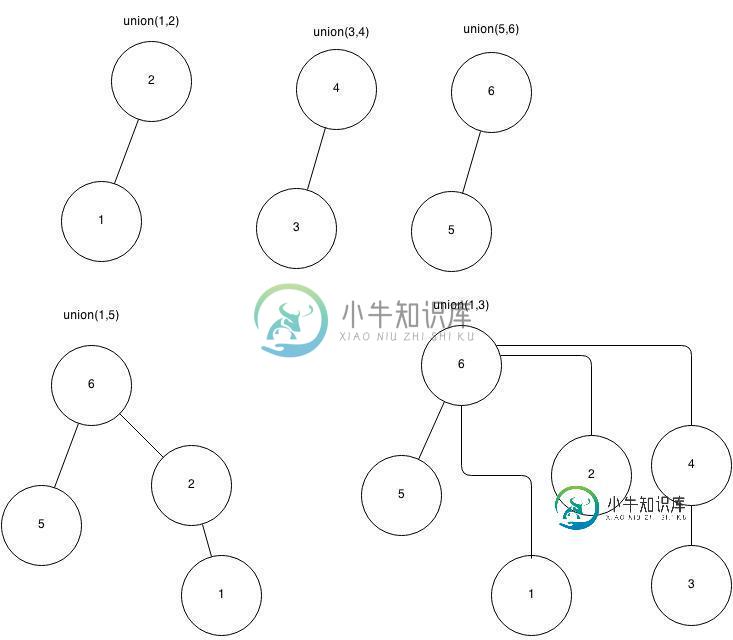
我很想有关于这个算法的任何提示或建议。

谢谢

Answer 1

< code>Union-Find Set查找操作的关键是路径压缩。

如果我们知道集合A的根是r1，而集合B的根是＜code>r2，那么将集合A和集合B连接在一起。最简单的方法是将集合B的根设为集合A的根，这意味着父亲[r2]=r1

但它并不那么“聪明”，当< code>r2的儿子，我们说< code>x，想知道它的根，< code>x问它的父亲< code>r2，然后父亲< code>r2问它自己的父亲< code>r1，blabla，直到根< code>r1。下次再次询问< code>x的根时，< code>x会询问其父< code>r1“我们的根是什么？”，则< code>r1没有必要再次重复之前的循环。由于< code>r1已经知道它的根是< code>r2，因此< code>r1可以直接将其返回给< code>x。

简而言之，x的根也是x的父亲的根。因此，我们得到了如何实现路径压缩（我认为递归更简单）：

int Find(int x)
{
    // initial each element's root as itself, which means father[x] = x;
    // if an element finds its father is itself, means root is found
    if(x == father[x])
        return father[x];
    int temp = father[x];
    // root of x's father is same with root of x's father's root
    father[x] = Find(temp);
    return father[x];
}

它是极高的性能，关于路径压缩查找操作的时间复杂度，请参阅：http://www.gabrielnivasch.org/fun/inverse-ackermann