如何在执行 BFS/DFS 算法时从遍历路径中找到最终路径

Question

我正在尝试解决一个问题，在一棵树上应用广度优先搜索算法和深度优先搜索算法，并找出这两种算法找到的遍历和最终路径。

我实际上感到困惑的是我如何计算这两种不同的路径？它们真的不同吗？

例如，考虑下面的树，

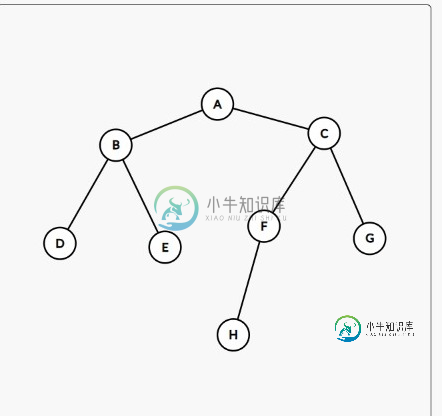
假设，我们的起始节点是A，目标节点是H

对于这两种算法，这就是我所感觉的穿越路径和最终路径

1. 对于BFS

遍历路径:A B C D E F G H

最终路径：A C F H

如果这就是它的工作方式，那么我如何才能找到最终的路径？找到遍历的路径非常容易，但找到最终的路径却不那么容易。

同样地，

遍历路径：A B D E C F G

最终路径：A C F H

同样，我如何从DFS的遍历路径中提取最终路径。

这实际上变得有点复杂。如果我的目标节点可以从两侧到达，该怎么办？在这种情况下，我如何找到最终路径？

例如，考虑以下方案，

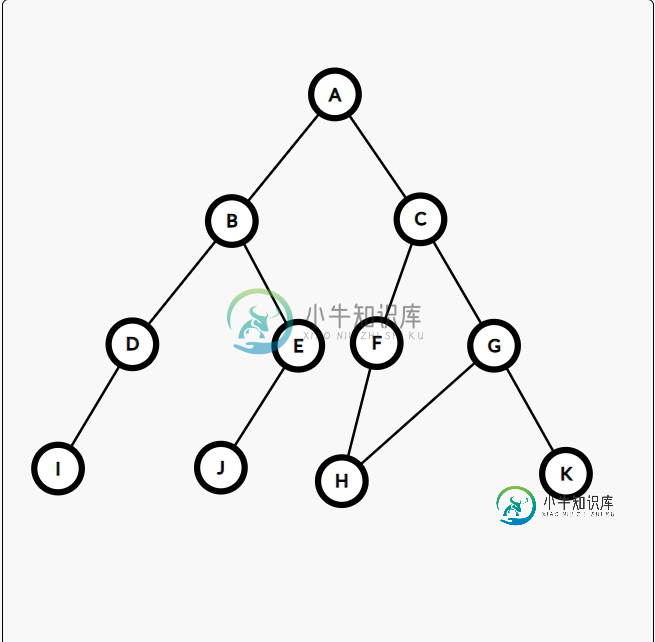
假设在这种情况下，我们的起始节点是A，目标节点也是H。

使用BFS和DFS都很容易计算遍历路径。

但是对于最终路径，“H”可以从两边到达，它可以从F到达，也可以从G到达

对于DFS，您可以将最终路径写成A C F G，因为从F节点开始，我们将首先到达H（因为G仍然未被探索，但是您仍然必须从遍历路径中提取此最终路径，我不知道该如何做）

但是对BFS来说，你不能这样做。那么，在这种情况下，我的最终道路会是什么呢？在这种情况下，应该有两条最终道路吗？

有人能帮我一下吗？

Answer 1

一种方法是维护目标到源节点的映射。每次前进时，记录前进的源节点。因此，在BFS的情况下，它看起来像：

parents = {
  'A': NULL,
  'B': 'A',
  'C': 'A',
  'D': 'B',
  'E': 'B',
  'F': 'C',
  'G': 'C' 
}

然后，从最后一个节点开始，向后重建路径:

node = target
path = []
while node:
   path.append(node)
   node = parents[node]

同样的方法适用于DFS和Dijkstra