删除二叉查找树中的节点
我现在正在读一本关于从二叉搜索树中删除节点的书,书中描述的过程对我来说似乎不必要地复杂。
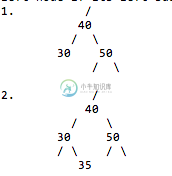
在1号情况下,如果我们删除40,它将替换为30;在 2 号情况下,如果我们删除 40,它将被替换 35。
但在书中,它说应该从要删除的节点的右子树中找到替换,这可能涉及一些复杂的操作。
我在这里遗漏了什么吗?请指出。
共有2个答案
在第1种情况下,如果删除节点40,它将被替换为50。
在第二种情况下,如果您删除节点40,它将被50取代。
所以基本上当我们删除任何有 2 个子节点的节点时,删除应该如下所示。我们去节点的右子节点,然后去那个孩子的最左边。
下图显示了一些示例,如何从二叉搜索树中删除节点。这也是取自一本书,但解释清楚。
您所指出的是正确的,删除的节点应替换为其顺序继承者(右子树中最左边的节点)或顺序继承者,左子树中的最右边的节点。这允许正确遍历树。大多数二进制搜索树数据结构允许以任何方式执行删除,但在某些特殊情况下,您可能希望实现删除,以使树保持平衡。
更多细节和示例代码可在维基百科上找到。
-
我试图从BST中删除最小节点,所以我在树中搜索,直到得到最小值(当root.leftnode为None时),然后将root.rightnode设置为根本身,以继续BST。 问题是,当我这样做之后检查树时,它不会显示曾经发生过的删除。 有人可以指出我正确的方向吗,任何建议都值得赞赏。
-
我正在阅读一本书,该书解释了如何从二元搜索树中删除节点,基本上如果我们有这棵树: 我们想删除节点4,书上说我应该: 在其右子树(即6)中找到4的继任者 交换4和6 从右子树中删除6 将4的左侧子树(在本例中仅为1)附加到新节点6 因此我们得到 然而,我想到了另一种方法来做到这一点: 找到4个右子树的最小元素(即6) 将4的左子树附加到6(它不会有左子树) 将父元素(10)附加到4的右侧元素(8)。
-
主要内容:什么是二叉排序树?,使用二叉排序树查找关键字,二叉排序树中插入关键字,二叉排序树中删除关键字,总结前几节介绍的都是有关静态 查找表的相关知识,从本节开始介绍另外一种查找表—— 动态查找表。 动态查找表中做查找操作时,若查找成功可以对其进行删除;如果查找失败,即表中无该关键字,可以将该关键字插入到表中。 动态查找表的表示方式有多种,本节介绍一种使用树结构表示动态查找表的实现方法—— 二叉排序树(又称为 “二叉查找树”)。 什么是二叉排序树? 二叉排序树要么是空 二叉树,要么具有如下特点:
-
我正在努力实现二叉搜索树。完成实现所需的功能之一是重新平衡功能。 根据规范,该功能的工作方式如下: rebalance() 方法应创建一个平衡树,从而将偏度降低为零。平衡树是指在整个树中,左子树和右子树的大小相差不超过1(即,每个子树也是平衡的)。 为了平衡树,rebalance() 方法应反复将根值移动到较小的子树,并将最小/最大值从较大的子树移动到根,直到树平衡。然后,它应该以递归方式平衡两个
-
我的删除方法由4个if语句组成,用于处理二叉查找树中的4种不同类型的删除。不确定哪里错了,但当我检查它时,它没有删除任何节点。如果赞赏,任何帮助。提前感谢' 我怀疑问题在于我试图将节点删除替换为空 }
-
当删除具有两个子节点的节点时,如果指示使用标准的二叉搜索树节点删除算法,我们应该将其替换为右子树的最小节点还是左子树的最大节点?

