两个圆形扇形的交点

Question

我正在尝试解决简单的任务，但我没有找到任何优雅的解决方案。

我基本上解决了两个圆形扇区的交集。每个扇区由（-pi， pi]范围内的2个角度（从atan2 func）给出。每个选择器占用的最大角度为179.999。所以每两个角度就可以知道圆形扇区的位置。

返回值应根据以下内容描述互交：

值

值

基本情况和一些例子见下图

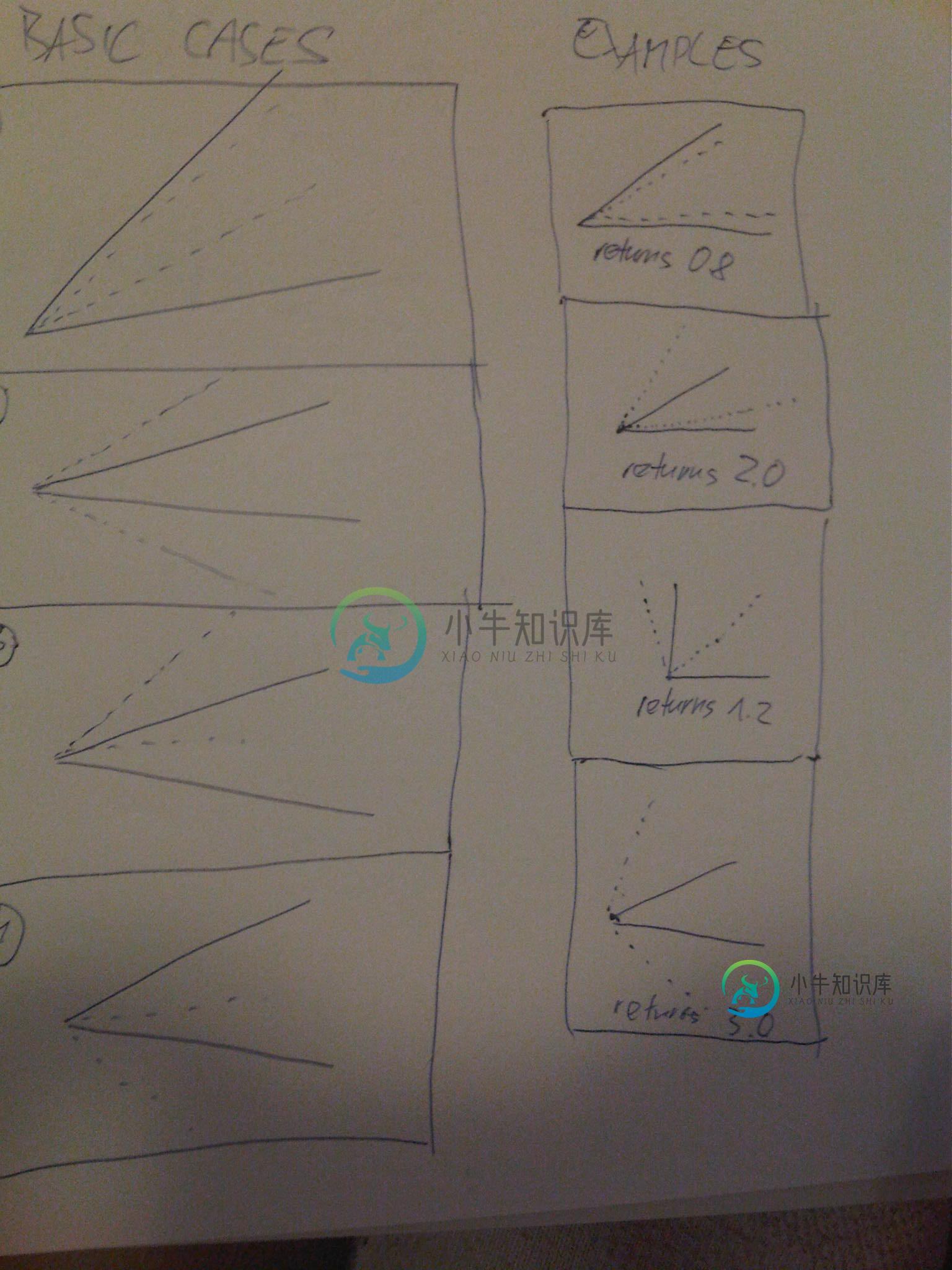
问题是有太多的案件需要处理，我正在寻找一些优雅的方法来解决。

只有当两个角度在单位圆的右侧时，我才能比较它们

if(x not in <-pi/2, pi/2>)
{
    c = getSign(x)*pi/2;
    x = c - (x - c);
}

但是占据单位圆两半部分的扇区存在一个问题…

案例实在是太多了...有人知道如何优雅地解决这个问题吗？（我使用c，但任何提示或伪代码都可以）




Answer 1

您可以执行以下操作：

>

将每个扇区归一化为形式（s_start，s_start），其中s _start＜/code＞位于（-pi，pi]），s _start位于（ ， ）。

对扇区进行排序（交换），以便s0_start

a)<代码> s1_start

b）s1_start

b1）s0_start2*pi

B2） s0_start 2*pi

因此，我们得到以下代码：

const double PI = 2.*acos(0.);
struct TSector { double a0, a1; };

// normalized range for angle
bool isNormalized(double a)
{ return -PI < a && a <= PI; }
// special normal form for sector
bool isNormalized(TSector const& s)
{ return isNormalized(s.a0) && s.a0 <= s.a1 && s.a1 < s.a0+PI; }

// normalize a sector to the special form:
// * -PI < a0 <= PI
// * a0 < a1 < a0+PI
void normalize(TSector& s)
{
   assert(isNormalized(s.a0) && isNormalized(s.a1));

   // choose a representation of s.a1 s.t. s.a0 < s.a1 < s.a0+2*PI
   double a1_bigger = (s.a0 <= s.a1) ? s.a1 : s.a1+2*PI;
   if (a1_bigger >= s.a0+PI)
     std::swap(s.a0, s.a1);
   if (s.a1 < s.a0)
     s.a1 += 2*PI;

   assert(isNormalized(s));
}

bool intersectionNormalized(TSector const& s0, TSector const& s1,
                            TSector& intersection)
{
  assert(isNormalized(s0) && isNormalized(s1) && s0.a0 <= s1.a0);

  bool isIntersecting = false;
  if (s1.a0 <= s0.a1) // s1.a0 inside s0 ?
  {
    isIntersecting = true;
    intersection.a0 = s1.a0;
    intersection.a1 = std::min(s0.a1, s1.a1);
  }
  else if (s0.a0+2*PI <= s1.a1) // (s0.a0+2*PI) inside s1 ?
  {
    isIntersecting = true;
    intersection.a0 = s0.a0;
    intersection.a1 = std::min(s0.a1, s1.a1-2*PI);
  }
  assert(!isIntersecting || isNormalized(intersection));

  return isIntersecting;
}

main()
{
  TSector s0, s1;
  s0.a0 = ...
  normalize(s0);
  normalize(s1);
  if (s1.a0 < s0.a0)
    std::swap(s0, s1);
  TSection intersection;
  bool isIntersection = intersectionNormalized(s0, s1, intersection);
}