gbdt推导

Answer 1

参考回答：

GBDT 全称为 Gradient Boosting Decision Tree。顾名思义,它是一种基于决策树(decision tree)实现的分类回归算法。

Gradient Descent: method of steepest descent

梯度下降作为求解确定可微方程的常用方法而被人所熟知。它是一种迭代求解过程,具体就是使解沿着当前解所对应梯度的反方向迭代。这个方向也叫做最速下降方向。具体推导过程如下。假定当前已经迭代到第 k 轮结束,那么第 k+1 轮的结果怎么得到呢?我们对函数 f 做如下一阶泰勒展开：

为了使得第k+1 轮的函数值比第 k 轮的小,即如下不等式成立。

则只需使:

按照这样一直迭代下去,直到 ∇f(xk)=0, xk+1=xk ，函数收敛,迭代停止。由于在做泰勒展开时,要求xk+1−xk 足够小。因此,需要γ比较小才行,一般设置为 0~1 的小数。

顺带提一下,Gradient Descent 是一种一阶优化方法,为什么这么说呢?因为它在迭代过程中不需要二阶及以上的信息。如果我们在泰勒展开时,不是一阶展开,而是二阶展开。那对应的方法就是另一个被大家所熟知的可微方程求解方法:Newton Method,关于牛顿法的详细内容,我们会在后续文章介绍。

Boosting: Gradient Descent in functional space

Boosting一般作为一种模型组合方式存在,这也是它在 GBDT 中的作用。那Boosting 与 gradient descent 有什么关系呢?上一节我们说到 gradient descent 是一种确定可微方程的求解方法。这里的可微有一个要求,就是说上文中的损失函数 f 针对模型 x 直接可微。因此模型x可以根据梯度迭代直接求解。而这种损失函数针对模型直接可微是一个很强的假设,不是所有的模型都满足,比如说决策树模型。现在我们回到第一节,将f(x)写的更具体一点：

f(x)=l(h(x,D),Y)

其中D 为数据特征;Y 为数据 label;h 为模型函数,解决由 D->Y 的映射,x为模型函数参数,即通常我们说的模型;l 为目标函数或损失函数。

以逻辑回归为例, x为权重向量, h模型函数展开为:

目标函数l展开为:

我们发现函数1对h可微,同时h对x可微,因此l对x可微。因此,我们可以通过 gradient descent的方式对x进行直接求解,而不用将h保存下来。然而,如果l对h可微,但h对x不可微呢?我们仍按照第一节的方法先对l进行泰勒展开,只不过不是针对x,而是对 h。为了简单起见,我们省略D,Y。

其中:

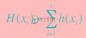
按照第一节的逻辑,我们不难得出如下迭代公式:

但别忘了,我们的目的不是求 h,而是 x。由于 h 对 x 不可微,所以 x 必须根据数据重新学习得到。而此时我们重新学习 x 的目标已经不是源目标 Y,而是原损失函数 l 在当前 H 处的梯度,即:

这个重新学习x的过程正是每个base weak learner所做的事情。而这种通过weak learner 拟合每一步迭代后的梯度,进而实现weak learner组合的方式,就是Boosting。又由于我们在求导过程中,损失函数l没法对模型x直接求导,而只能对模型函数h求导。因此 Boosting又有一个别名:“函数空间梯度下降“。

此外,你可能会听过boosting的可加性(additive)。这里顺便提一句,可加性指的是 h 的可加,而不是x的可加。比如x是决策树,那两棵决策树本身怎么加在一起呢?你顶多把他们并排放在一起。可加的只是样本根据决策树模型得到的预测值 h(x,D)罢了。

Decision Tree: the based weak learner

Boosting 的本质就是使用每个weak learner来拟合截止到当前的梯度。则这里的D,还是原来数据中的D,而Y已经不是原来的Y了。而GBDT 中的这个weak learner 就是一棵分类回归树(CART)。因此我们可以使用决策树直接拟合梯度:∇l(H(xt))。此时我们要求的x就变成了这样一棵有k个叶子节点的、使得如下目标函数最小化的决策树:

其中T为目标∇l(H(xt)),W为每个叶子节点的权重,L为叶子节点集合。容易求得每个叶子节点的权重为归属到当前叶子节点的样本均值。即 :

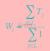
每个样本的预测值即为其所归属的叶子节点的权重,即h(xt+1)