计算图(Computational Graphs)
反向传播通过使用计算图在Tensorflow,Torch,Theano等深度学习框架中实现。 更重要的是,理解计算图上的反向传播结合了几种不同的算法及其变体,例如通过时间的backprop和具有共享权重的backprop。 一旦将所有内容转换为计算图,它们仍然是相同的算法 - 只是在计算图上反向传播。
什么是计算图
计算图被定义为有向图,其中节点对应于数学运算。 计算图是表达和评估数学表达式的一种方式。
例如,这是一个简单的数学方程式 -
$$p = x+y$$
我们可以如下绘制上述等式的计算图。
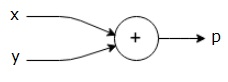
上述计算图具有加法节点(具有“+”符号的节点),其具有两个输入变量x和y以及一个输出q。
让我们再举一个例子,稍微复杂一些。 我们有以下等式。
$$g = \left (x+y \right ) \ast z $$
上述等式由以下计算图表示。
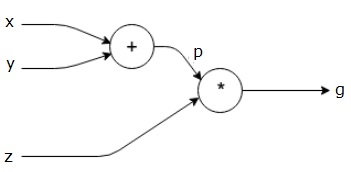
计算图和反向传播
计算图和反向传播都是深度学习训练神经网络的重要核心概念。
前进通行证
前向传递是用于评估由计算图表示的数学表达式的值的过程。 执行正向传递意味着我们将变量的值从左(输入)向前传递到输出所在的右侧。
让我们通过给所有输入赋予一些价值来考虑一个例子。 假设,所有输入都给出以下值。
$$x=1, y=3, z=−3$$
通过将这些值赋给输入,我们可以执行正向传递并为每个节点上的输出获取以下值。
首先,我们使用x = 1和y = 3的值,得到p = 4。
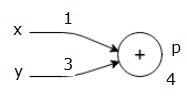
然后我们使用p = 4和z = -3来得到g = -12。 我们从左到右前进。
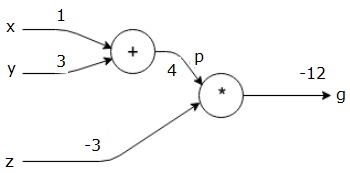
落后目标
在向后传递中,我们的目的是计算每个输入相对于最终输出的梯度。 这些梯度对于使用梯度下降训练神经网络至关重要。
例如,我们需要以下渐变。
期望的渐变
$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$
Backward pass (backpropagation)
我们通过找到最终输出相对于最终输出(本身!)的导数来开始向后传递。 因此,它将导致身份派生,并且该值等于1。
$$\frac{\partial g}{\partial g} = 1$$
我们的计算图现在看起来如下所示 -
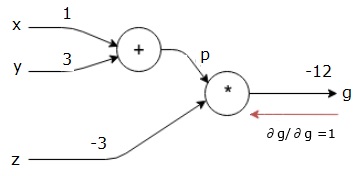
接下来,我们将执行向后传递“*”操作。 我们将计算p和z处的梯度。 由于g = p * z,我们知道 -
$$\frac{\partial g}{\partial z} = p$$
$$\frac{\partial g}{\partial p} = z$$
我们已经知道了前向传球中z和p的值。 因此,我们得到 -
$$\frac{\partial g}{\partial z} = p = 4$$
和
$$\frac{\partial g}{\partial p} = z = -3$$
我们想要计算x和y处的梯度 -
$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$
但是,我们希望有效地做到这一点(尽管在此图中x和g只有两跳,想象它们彼此相距很远)。 为了有效地计算这些值,我们将使用区分链规则。 从连锁规则来看,我们有 -
$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$
$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$
但我们已经知道dg/dp = -3,dp/dx和dp/dy很容易,因为p直接取决于x和y。 我们有 -
$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$
因此,我们得到 -
$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$
另外,对于输入y -
$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$
向后执行此操作的主要原因是,当我们必须计算x处的梯度时,我们仅使用已计算的值和dq/dx(节点输出相对于同一节点输入的导数)。 我们使用本地信息来计算全球价值。
训练神经网络的步骤
按照以下步骤训练神经网络 -
对于数据集中的数据点x,我们使用x作为输入进行正向传递,并将成本c计算为输出。
我们从c开始向后传递,并计算图中所有节点的渐变。 这包括表示神经网络权重的节点。
然后我们通过W = W-学习率*梯度来更新权重。
我们重复此过程,直到满足停止标准。

