java图的深度优先遍历实现随机生成迷宫

最近经常在机房看同学在玩一个走迷宫的游戏,比较有趣，自己也用java写一个实现随机生成迷宫的算法，其实就是一个图的深度优先遍历算法.基本思想就是，迷宫中的每个点都有四面墙，然后呢。

1、从任意一点开始访问(我的算法中固定是从(0,0)点开始),往四个方向中的随机一个访问(每访问到一个可访问的点,就去掉该点的那个方向的墙),被访问点继续以这种方识向下进行访问。

2、对每个被访问的点都被标识为已访问,当一个点对某个方向进行访问时我们首先会判断被访问点是否已被访问,或者触到边界.如果该点四个方向皆已访问或已无法访问,就退回上一个点。上一个点继续这个过程。 

这样一次遍历下来，可以确定每个点都被访问过，而且由于每次访问的方向都是随机，这就会形成许多不同遍历情况，同时每两个点之间的路径是唯一，也就形成不同的迷宫，且是起点到终点只有唯一路径，这是由于图的深度遍历算法的特点所决定的。算法的实现上,主要是利用栈,第一次,先把第一个点压进栈里,每访问到一个点,就把该点压进栈里,我们再对栈顶的点进行四个方向的随机访问,访问到新点,又把新点压进去,一旦这个点四个方向都无法访问了,就让该点退栈,再对栈顶的点的四个方向进行访问,以此类推,直到栈里的点都全部退出了,我们的遍历就成功了,这是一个递归的过程,这个算法自然可以用递归的方法来实现,不过这里我这样做,而是手工用一个数组作为栈来实现,呵呵~~说了这么多,也不知道自己要表达的有没表达出来。不过我感觉我的具体代码设计还是写的不好，还有很多地方缺乏完善和优化,权当是算法练习,以下是两个关键类的核心代码，至于表示层的代码就不贴出来了，因为那些都很琐碎。

下面是效果图:

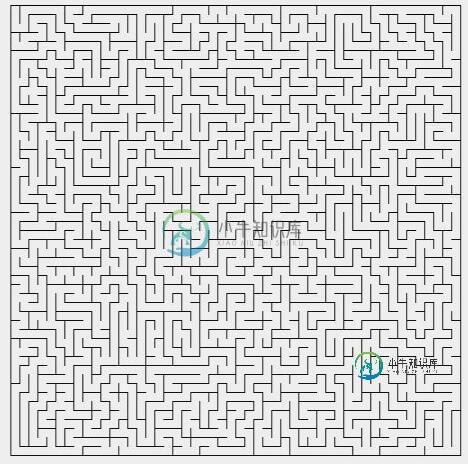
迷宫的类：

//作者:zhongZw 
//邮箱:zhong317@126.com 
package cn.zhongZw.model; 
import java.util.ArrayList; 
import java.util.Random; 
public class MazeModel { 
 private int width = 0; 
 private int height = 0; 
 private Random rnd = new Random(); 
 
 public MazeModel() { 
  this.width = 50; //迷宫宽度 
  this.height = 50; //迷宫高度 
 } 
 public int getWidth() { 
  return width; 
 } 
 public void setWidth(int width) { 
  this.width = width; 
 } 
 public int getHeight() { 
  return height; 
 } 
 public void setHeight(int height) { 
  this.height = height; 
 } 
 public MazeModel(int width, int height) { 
  super(); 
  this.width = width; 
  this.height = height; 
 } 
 public ArrayList < MazePoint > getMaze() { 
  ArrayList < MazePoint > maze = new ArrayList < MazePoint > (); 
  for (int h = 0; h < height; h++) { 
   for (int w = 0; w < width; w++) { 
    MazePoint point = new MazePoint(w, h); 
    maze.add(point); 
   } 
  } 
  return CreateMaze(maze); 
 } 
 private ArrayList < MazePoint > CreateMaze(ArrayList < MazePoint > maze) { 
  int top = 0; 
  int x = 0; 
  int y = 0; 
  ArrayList < MazePoint > team = new ArrayList < MazePoint > (); 
  team.add(maze.get(x + y * width)); 
  while (top >= 0) { 
   int[] val = new int[] { 
    -1, -1, -1, -1 
   }; 
   int times = 0; 
   boolean flag = false; 
   MazePoint pt = (MazePoint) team.get(top); 
   x = pt.getX(); 
   y = pt.getY(); 
   pt.visted = true; 
 
   ro1: while (times < 4) { 
    int dir = rnd.nextInt(4); 
    if (val[dir] == dir) 
     continue; 
    else 
     val[dir] = dir; 
 
 
 
 
    switch (dir) { 
    case 0: // 左边 
     if ((x - 1) >= 0 && maze.get(x - 1 + y * width).visted == false) { 
      maze.get(x + y * width).setLeft(); 
      maze.get(x - 1 + y * width).setRight(); 
      team.add(maze.get(x - 1 + y * width)); 
      top++; 
      flag = true; 
      break ro1; 
 
     } 
     break; 
    case 1: // 右边 
     if ((x + 1) < width && maze.get(x + 1 + y * width).visted == false) { 
 
      maze.get(x + y * width).setRight(); 
      maze.get(x + 1 + y * width).setLeft(); 
      team.add(maze.get(x + 1 + y * width)); 
      top++; 
      flag = true; 
      break ro1; 
     } 
     break; 
    case 2: // 上边 
     if ((y - 1) >= 0 && maze.get(x + (y - 1) * width).visted == false) { 
      maze.get(x + y * width).setUp(); 
      maze.get(x + (y - 1) * width).setDown(); 
      team.add(maze.get(x + (y - 1) * width)); 
      top++; 
      flag = true; 
      break ro1; 
     } 
     break; 
    case 3: // 下边 
     if ((y + 1) < height && maze.get(x + (y + 1) * width).visted == false) { 
      maze.get(x + y * width).setDown(); 
      maze.get(x + (y + 1) * width).setUp(); 
      team.add(maze.get(x + (y + 1) * width)); 
      top++; 
      flag = true; 
      break ro1; 
     } 
     break; 
    } 
    times += 1; 
   } 
   if (!flag) { 
    team.remove(top); 
    top -= 1; 
   } 
 
  } 
 
  return maze; 
 } 
} 

迷宫

//作者:zhongZw 
//邮箱:zhong317@126.com 
package cn.zhongZw.model; 
import java.util.*; 
import java.lang.*; 
public class MazePoint { 
 private int left = 0; 
 private int right = 0; 
 private int up = 0; 
 private int down = 0; 
 private int x; 
 private int y; 
 public boolean visted; 
 public MazePoint(int x, int y) { 
  this.x = x; 
  this.y = y; 
 } 
 public int getLeft() { 
  return left; 
 } 
 
 public void setLeft() { 
  this.left = 1; 
 } 
 public int getRight() { 
  return right; 
 } 
 public void setRight() { 
  this.right = 1; 
 } 
 public int getUp() { 
  return up; 
 } 
 
 public void setUp() { 
  this.up = 1; 
 } 
 public int getDown() { 
  return down; 
 } 
 
 public void setDown() { 
  this.down = 1; 
 } 
 public int getX() { 
  return x; 
 } 
 public void setX(int x) { 
  this.x = x; 
 } 
 public int getY() { 
  return y; 
 } 
 public void setY(int y) { 
  this.y = y; 
 } 
 
 
} 

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。