python最小生成树kruskal与prim算法详解

kruskal算法基本思路：先对边按权重从小到大排序，先选取权重最小的一条边，如果该边的两个节点均为不同的分量，则加入到最小生成树，否则计算下一条边，直到遍历完所有的边。

prim算法基本思路：所有节点分成两个group，一个为已经选取的selected_node（为list类型），一个为candidate_node，首先任取一个节点加入到selected_node，然后遍历头节点在selected_node，尾节点在candidate_node的边，选取符合这个条件的边里面权重最小的边，加入到最小生成树，选出的边的尾节点加入到selected_node，并从candidate_node删除。直到candidate_node中没有备选节点（这个循环条件要求所有节点都有边连接，即边数要大于等于节点数-1，循环开始前要加入这个条件判断，否则可能会有节点一直在candidate中，导致死循环）。

#coding=utf-8
class Graph(object):
  def __init__(self, maps):
    self.maps = maps
    self.nodenum = self.get_nodenum()
    self.edgenum = self.get_edgenum()
 
  def get_nodenum(self):
    return len(self.maps)
 
  def get_edgenum(self):
    count = 0
    for i in range(self.nodenum):
      for j in range(i):
        if self.maps[i][j] > 0 and self.maps[i][j] < 9999:
          count += 1
    return count
 
  def kruskal(self):
    res = []
    if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
      return res
    edge_list = []
    for i in range(self.nodenum):
      for j in range(i,self.nodenum):
        if self.maps[i][j] < 9999:
          edge_list.append([i, j, self.maps[i][j]])#按[begin, end, weight]形式加入
    edge_list.sort(key=lambda a:a[2])#已经排好序的边集合
    
    group = [[i] for i in range(self.nodenum)]
    for edge in edge_list:
      for i in range(len(group)):
        if edge[0] in group[i]:
          m = i
        if edge[1] in group[i]:
          n = i
      if m != n:
        res.append(edge)
        group[m] = group[m] + group[n]
        group[n] = []
    return res
 
  def prim(self):
    res = []
    if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
      return res
    res = []
    seleted_node = [0]
    candidate_node = [i for i in range(1, self.nodenum)]
    
    while len(candidate_node) > 0:
      begin, end, minweight = 0, 0, 9999
      for i in seleted_node:
        for j in candidate_node:
          if self.maps[i][j] < minweight:
            minweight = self.maps[i][j]
            begin = i
            end = j
      res.append([begin, end, minweight])
      seleted_node.append(end)
      candidate_node.remove(end)
    return res
 
max_value = 9999
row0 = [0,7,max_value,max_value,max_value,5]
row1 = [7,0,9,max_value,3,max_value]
row2 = [max_value,9,0,6,max_value,max_value]
row3 = [max_value,max_value,6,0,8,10]
row4 = [max_value,3,max_value,8,0,4]
row5 = [5,max_value,max_value,10,4,0]
maps = [row0, row1, row2,row3, row4, row5]
graph = Graph(maps)
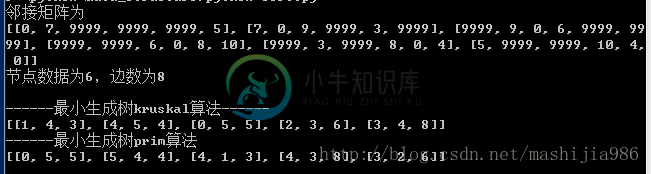
print('邻接矩阵为\n%s'%graph.maps)
print('节点数据为%d，边数为%d\n'%(graph.nodenum, graph.edgenum))
print('------最小生成树kruskal算法------')
print(graph.kruskal())
print('------最小生成树prim算法')
print(graph.prim())

初始的图如下。

运行结果如下。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。